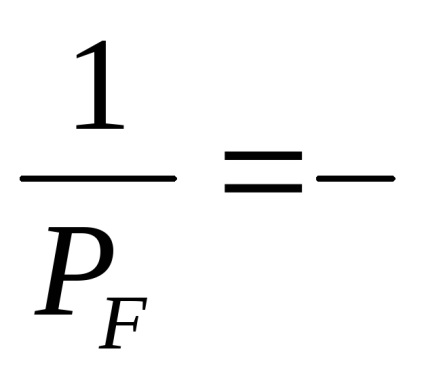A háromszögelés kiegyenlítésének jellemzői az irányokban
Ha a háromszögelés kiegyenlíti a korrekciós egyenletek irányát, a koordináták hozzávetőleges értékeire vonatkozó korrekciók mellett korrekciókat végzünk az állomások irányított szögeként

ahol C és A az orientációs szögek korrekciós vektorainak koefficiens mátrixai


Ez megfelel a normál egyenletek rendszerének
hol van a mért irányok tömegmátrixa.
A helyettesítési módszer alkalmazása és megszüntetése

Ezt a transzformált rendszert más módon lehet elérni.
Hagyja, hogy a korrekciók következő egyenletei megfeleljenek az i állomáson mért irányoknak
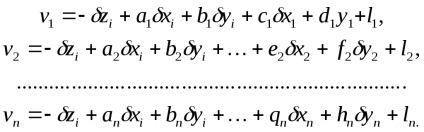
A következő egyenletrendszerek felelnek meg:
Ha kivonjuk a rendszer első egyenletéből (134)
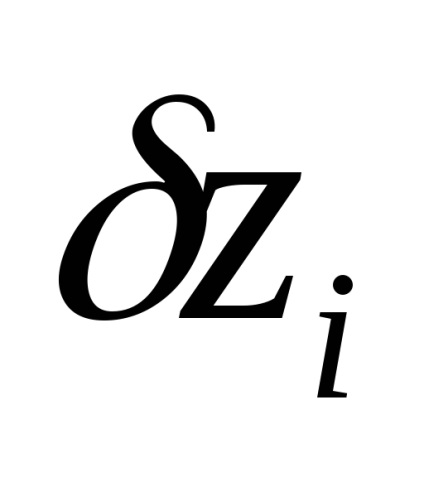
és helyettesíti a többi, akkor megkapjuk az egyenértékű rendszert
Ebből kiindulva könnyű látni, hogy a normál egyenletek mátrixa a meglévő korrekciós egyenletek alapján összeállítható az úgynevezett teljes egyenlet minden egyes állomásán
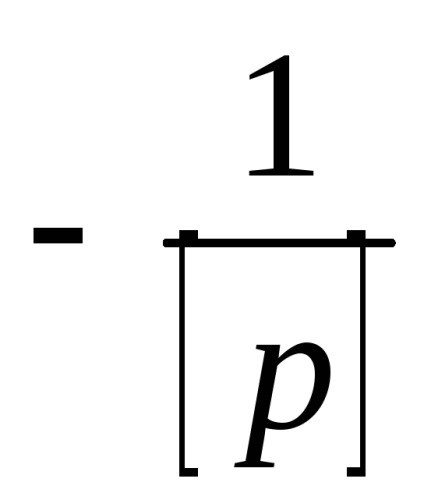
Példa egy geodéziai hálózat parametrikus módszerrel történő beállítására
A 18. ábrán látható geodéziai hálózat kiegyenlítése. 21 a kiegyenlítés példáján a korrelációs módszerrel.
A D és E pontok közelítő koordinátái a következők
Felhívjuk a figyelmet arra, hogy a geodéziai hálózatokban végzett mérésekből kiderül.
Először a korrekciós egyenletek szabad feltételeinek kiszámításához a meghatározott pontok hozzávetőleges koordinátáinak értékeitől és a kezdeti koordinátáktól származó értékekből kell kiszámítani az oldalirányok irányszögeit és hosszát a feltételezett közelítő koordinátáknak megfelelő pontossággal. Ehhez a reverz geodéziai problémákat a képletek oldják meg
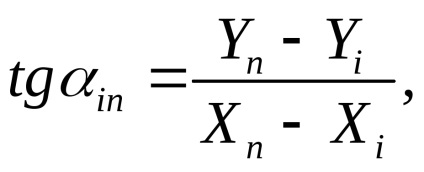
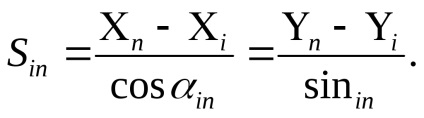
ahol i, n a tételek száma.
Az oldalak hosszának és az előzetes koordináták irányszögeinek pontos kiszámítása után kiszámítják a korrekciós egyenletek szabad feltételeit (15. táblázat). Ugyanebben a táblázatban az együtthatók
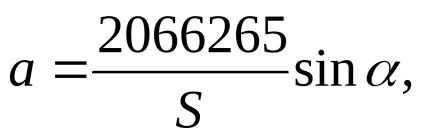
szükséges a korrekciós egyenletek koefficienseinek mátrixának kialakításához.
A (115) és a (137) bekezdésnek megfelelően az egyes mért irányokhoz tartozó korrekciós egyenletek formája lesz
és a mért oldalon a forma (108).
A teljes hálózatra vonatkozó korrekciós egyenletek rendszere a 16. táblázatban található.
Ugyanazon a helyen, minden egyes állomás esetében a forma (136) összes egyenlete is összeállítható.
A normál egyenletek rendszere
a 17. táblázatban látható.
A normál egyenletek rendszere
A 17. táblázat csak a normál egyenletek mátrixának felső háromszöget mutatja
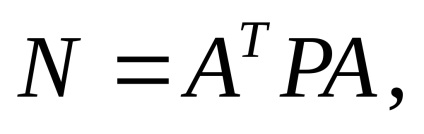
vektor szabad kifejezések
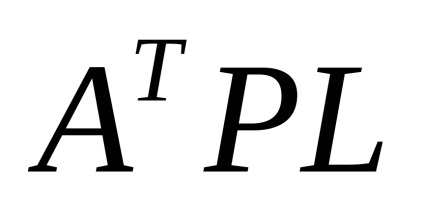
A normál egyenletek rendszere ugyanúgy fordul elő, mint a normál korrelációs egyenletek rendszere. De ebben az esetben a megfelelő oszlopokat megszorozzák a mérési súlyokkal, nem pedig a reciprokokkal, mint a korrelációs módszerrel.
A normál egyenletek megoldását a Gauss-rendszer szerint a 18. táblázatban adjuk meg.
A meghatározott D és E pont koordinátáinak és hozzávetőleges koordinátáinak a kapott korrekciói alapján a végső értékeket

A (135) alapján kiszámítjuk az egyes állomás tájolási szögének korrekcióját.
A normál egyenletek megoldása a Gauss-rendszer szerint
Figyelembe véve ezt a korrekciót és a korrekció értékét a meghatározott pontok hozzávetőleges koordinátáihoz, az utasítások korrekcióinak egyenlete alapján (138) kiszámítjuk az utasítások korrekcióit. A mért oldali korrekciókat úgy számoljuk ki, hogy a koordináta korrekciókat az oldalsó korrekciók egyenleteire (108) helyettesítjük. Számításukat a 16. táblázatban adjuk meg.
A számítások pontosságával kapott korrekcióknak egybe kell esniük a kiegyenlítő korrelációs módszer által talált korrekciókkal.
A tömegegység átlagos négyzetes hibájának kiszámítását a (94) képlet segítségével is elvégezzük. Általában a paraméteres módszerben a többletmérések számát a képlet határozza meg
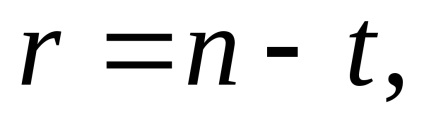
ahol n a korrekciós egyenletek száma, t az ismeretlen paraméterek száma. Ha az irányok kiegyenlítésre kerülnek, a t számot a képlet segítségével számítják ki
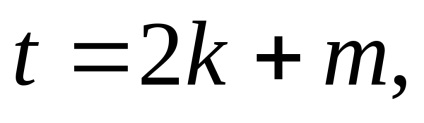
ahol k a meghatározandó pontok száma, m az az állomások száma, ahonnan az irányokat mértük. Ha az irány minden pontján csak egyszer mértük, akkor az m szám megegyezik az összes pont számával, beleértve a kezdeti értékeket is. Ez a szám megegyezik az összes irányított szög számával, azaz a mért iránygerendák száma.
A tömegegység átlagos négyzetes hibájának értéke a standard 128 () becslése. Továbbá, a (128) képlet segítségével kiszámíthatjuk a beállítások pontossági becslését a beállítás után. A paraméteres módszerben célszerű becsülni a meghatározott pontok pontosságát a (131) képlet segítségével. Ebben az esetben meg kell fordítani az N. normál egyenletek mátrixát.
Kezelése különböző módon hajtható végre. A legalkalmasabb módszer a módosított Jordan kivétel.
Ennek lényege a következő:
1) A kezdeti mátrixban a felbontó elem
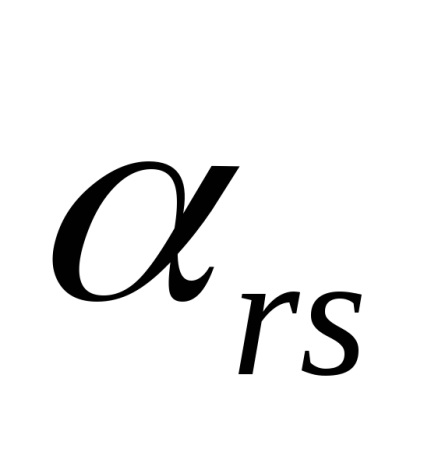
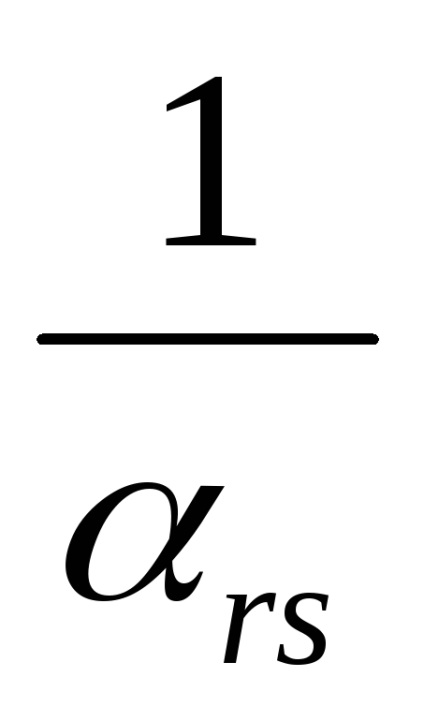
2) Az r rezolváló string többi eleme egy feloldó elemre oszlik.
3) Az S rezolváló oszlop fennmaradó elemei egy feloldó elemre vannak felosztva, és megfordulnak.
4) a többi elemet az alábbi képlet adja meg:
A számításokat célszerű két tizedesjegy pontosságának megtartásával elvégezni.
A Jordan kivételének első lépéseként a 4.17 átlós elemet alkalmazzák a felbontóként.
Az eredmény egy mátrix
A második lépésben a mátrix (141) második transzformált diagonális eleme feloldódik, azaz E. 7,90.
A harmadik lépésben a 9142 mátrix diagonális elemét alkalmazzuk rezolverként. 9.75.
A negyedik lépésben, azaz. az utolsó, felbontó elem 8,13 lesz.
A végeredmény mátrix formájában jelenik meg
amely a mátrix inverze (139) lesz.
Az inverszió helyességének ellenőrzése a (139) és (144) mátrixok termékének azonosító mátrixának egyenlõsége 0,1 pontossággal. Ezenkívül, amikor a Jordan kivételeinek egyik lépcsőjéről a másikra változnak, meg kell figyelni a kialakuló mátrixok szimmetriáját. Csak a bal oldali rezolváló karakterláncban és a felbontó elem felett lévő feloldó oszlopban csak a jelek különböznek.
Végül a (131) képlet szerint megtaláljuk
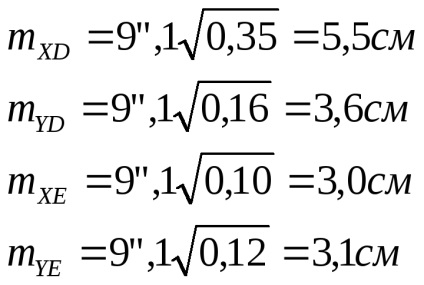
A D és E pontok általános helyzetében hibák lesznek
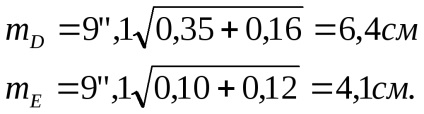
A 17. táblázat mátrixának (144) és A T PL oszlopának segítségével a (130) képlet segítségével korrekciókat találhatunk a meghatározott pontok hozzávetőleges koordinátáihoz. a normál Gauss-egyenletek megoldásához a 18. táblázatban kiszámított értékek megegyeznek.
Az egyes funkciók pontosságának becslése a Gauss-képlet segítségével is elvégezhető. Ebben az esetben a súlyfüggvény kiszámítása a meghatározandó paramétereknek megfelelően történik
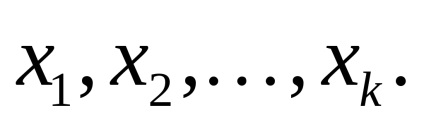
ahol
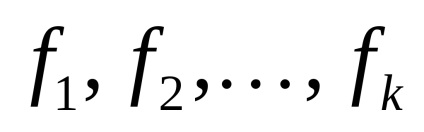
Ebben a problémában az ilyen paraméterek a meghatározott pontok hozzávetőleges koordinátáihoz való korrekciók,
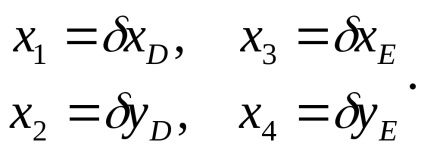
E függvény inverz súlya egyenlő