Chernookan a
Külön megállapodással a Quantum folyóirat szerkesztõségével és szerkesztõbizottságával
A mechanikai problémák megoldása során felbecsülhetetlen értékű lehet az anyagpontok rendszerének tömegközéppontjának használata. Néhány feladat nem megoldható anélkül, hogy erre a koncepcióra támaszkodna, a segítségnyújtás mások megoldása sokkal könnyebbé és láthatóbbá válhat.
Mielőtt konkrét problémákat vitatunk meg, felidézzük a tömegközéppont fő tulajdonságait, példákkal illusztráljuk őket.
Az anyagpontok rendszerének tömegközéppontja (tömegközéppontja) egy olyan pont, amely a tömegek eloszlását jellemzi egy olyan rendszerben, amelynek koordinátáit formulák
Itt vagyok a rendszer alkotó anyagpontok tömegei, xi. yi. zi ezeknek a pontoknak a koordinátái. A sugárvektor fogalmát ismerő olvasók inkább a vektoros jelölést preferálják:
1. példa. Találjuk meg a tömegközéppont helyzetét, a legegyszerűbb rendszert, amely két pontból áll, amelyek m1 és m2 tömege és a közöttük l távolság (ld.
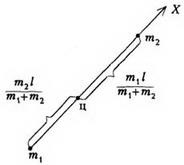
Az X tengelynek az első ponttól a második pontig történő irányításával azt találjuk, hogy az első ponttól a tömegközéppontig terjedő távolság (azaz a tömegközéppont koordinátája) egyenlő, és a tömegközéptől a második pontig terjedő távolság egyenlő. a távolságok aránya a tömegek arányához képest. Ezért ebben az esetben a tömegközéppont helye egybeesik a súlyponttal.
1) A tömegközéppont helyzete nem változik, ha a rendszer bármely részét egy ponttal helyettesítik, amelynek tömege megegyezik az alrendszer tömegével és tömegközéppontjában.
2. példa. Tartson egy sík homogén háromszöget, és keresse meg a tömegközéppont helyzetét. Oszd meg a háromszöget az egyik oldalával párhuzamos vékony csíkokra, és helyezze az egyes szalagokat egy középső pontra. Mivel az ilyen pontok a háromszög középső pontján helyezkednek el, a tömegközéppontnak a mediánra is rá kell terjednie. Ismételjük az egyes oldalak érveit, azt találjuk, hogy a tömegközéppont a mediánok metszéspontjában található.
2) A tömegközéppont sebességét az (1) mindkét oldali időszármazékának figyelembe vételével találjuk meg:
hol van a rendszer lendülete, m a rendszer teljes tömege. Látható, hogy a zárt rendszer tömegközéppontjának sebessége állandó. Ezért, ha egy mozgó hivatkozási keretet társítunk a tömegközépponttal, akkor inerciális lesz.
3. példa Egy egyenletes hosszúságú rúdot függőlegesen egy sík síkra (2. Ábra) kell elhelyezni és elengedni. A leesés folyamatában mind a lendülete vízszintes összetevője, mind a tömegközéppont sebességének vízszintes összetevője nulla marad. Ezért a bukás pillanatában a rúd középpontja azon a helyen lesz, ahol a pálca eredetileg állt, és a rúd vége vízszintesen mozog.
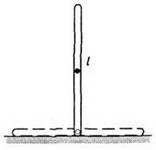
3) A tömegközéppont gyorsulása megegyezik a sebességének az időhöz viszonyított sebességével:
ahol az egyenlet jobb oldalán csak külső erők vannak, hiszen az összes belső erőt a Newton harmadik törvénye szerint kötötték fel. Úgy találjuk, hogy a tömegközéppont úgy mozog, mint egy képzeletbeli pont a tömeg tömegével megegyező tömeggel mozog a keletkező külső erő hatására. Valószínűleg ez a tömegközéppont fizikai tulajdonsága.
4. példa Ha egy botot dobol és forgat, a bot (tömegközéppont) tömegközéppontja folyamatosan gyorsul a parabola mentén (3.
4) Hagyja a pontrendszer homogén gravitációs mezőt. Ezután a tömeg összes súlyát a tömegközépponton átmenő tengelyhez viszonyítva nulla. Ez azt jelenti, hogy a gravitációs hatások eredménye a tömegközépponton keresztül halad át, azaz a tömegközéppont is a súlypont.
5) A homogén gravitációs tér pontrendszerének potenciális energiáját a képletből számítjuk ki
ahol h, a rendszer tömegközéppontjának magassága.
5. Példa Ha egy homokos mélységű mélységű ásót ásunk, és a talajt a felszín mentén terítjük, annak potenciális energiája növekszik, ahol m a kivont talaj tömege.
6) És még egy hasznos tulajdonsága a tömegközéppontnak. A pontrendszer kinetikus energiáját két kifejezés összegeként ábrázolhatjuk: a rendszer teljes transzlációs mozgásának kinetikus energiája és a mozgás kinetikus energiája a tömegközépponthoz kapcsolódó referenciakerethez viszonyítva:
6. példa A kerék mozgásának kinetikus energiája a vízszintes felületen csúszás nélkül, a sebességgel υ
mivel a relatív mozgás ebben az esetben egy tiszta forgás, amelyre a kerék pontjai lineáris sebessége υ (az alsó pont teljes sebessége nulla legyen).
Most megkezdjük a tömegközéppont felhasználásával kapcsolatos feladatok elemzését.
Probléma 1. Homogén rúd fekszik sima vízszintes felületen. Két egyenlő nagyságú, de vízszintes erővel ellentétes erőt alkalmaznak a rúdra: egy erő a rúd közepére, a másik végén (4. ábra). Ami azt a pontot illeti, hogy a rúd kezd megfordulni?
Első pillantásra úgy tűnhet, hogy a forgási tengely olyan pont, amely középen fekszik az erők alkalmazási pontjain. A (3) egyenlet azonban azt mutatja, hogy mivel a külső erők összege nulla, a tömegközéppont gyorsulása nulla. Ezért a rúd középpontja nyugalomban marad, azaz a forgás tengelyeként szolgálnak.
2. probléma. Egy vékony, homogén hosszúságú l hosszúságú rudat és egy m tömeget sima vízszintes felület mentén mozgatunk úgy, hogy a transzlációs mozgással és egyidejűleg az ω szögsebességgel elforduljon. Keresse meg a rúd feszességét az x távolság függvényében.
Menjünk át az inerciális referenciakeretre, amely a rúd középpontjához kapcsolódik. Tekintsük egy rúddarab mozgását, amely a rúd (a középponttól x távolságra elhelyezkedő) és a vége közötti távolság (5.
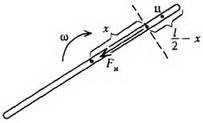
Ennek a darabnak az egyetlen külső ereje a kívánt Fn feszítőerő. a tömeg egyenlő, és tömegközéppontja a kerület mentén gyorsuló sugárral mozog. A kiválasztott darab tömegközéppontjának mozgásának egyenletét kiírva kapjuk meg
3. feladat: A kettős csillag kétkomponensű csillagból áll, melyek tömege m1 és m2. amelynek távolsága nem változik, és egyenlő L-vel. Keresse meg a kettős csillag forgásának időtartamát.
Tekintsük a komponens csillag mozgását egy inerciális referenciakeretre, amely összekapcsolódik egy bináris csillag tömegével. Ebben a referenciakeretben a csillagok ugyanolyan szögsebességgel mozognak különböző sugarak körvonala mentén (6.
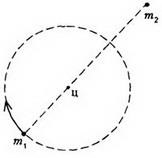
Az m1 tömegű csillag csillag forgásának sugara egyenlő (lásd az 1. példát), és centripetális gyorsulását egy másik csillag vonzásának ereje hozza létre:
Látjuk, hogy a kettős csillag forgási ideje megegyezik
és a bináris csillag teljes tömege határozza meg, függetlenül attól, hogyan oszlik meg a komponens csillagok között.
4. probléma. Két és két méter közötti tömegeket egy l hosszúságú, súlytalan fonal összeköt, és egy sima vízszintes sík mentén mozog. Egy bizonyos időpontban a 2m tömegsebesség nulla, és a tömegsebesség m egyenlő a υ-vel, és merőleges az izzószálra (7. Keresse meg a szál feszességét és a rendszer forgási időtartamát.
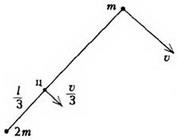
A rendszer tömegközéppontja a 2 m tömegtől távol, és sebességgel mozog. A tömegközépponthoz kapcsolt referenciakeretben egy 2 m tömegű pont a kerület mentén mozgatható sebességgel. Ezért a forgás időtartama megegyezik (ellenőrizzük, hogy ugyanazt a választ kapjuk, ha egy m tömegpontot vesszük figyelembe). Az izzóspirál feszültségét a két pont közül bármelyik mozgás egyenletéből találjuk:
5. probléma Sima vízszintes síkban két azonos tömegű m-es rúd van, amelyeket k keménységű könnyű rugó csatlakoztat (8. ábra). Az első sávot a υ0 sebesség a második sáv irányában kapja. Ismertesse a rendszer mozgását. Miután a rugó deformációja először elérte maximális értékét?
A rendszer tömegközéppontja állandó sebességgel mozog. A tömeges referenciakeret középpontjában az egyes sávok kezdeti sebessége egyenlő, és a fele rugó merevsége, amely összekapcsolja a rögzített tömegközépponttal, 2k (a rugó merevsége fordítottan arányos annak hosszával). Az ilyen oszcillációk időtartama:
és az egyes oszlopok oszcillációinak amplitúdója, amely az energia megőrzésének törvényéből származik
Első alkalommal a deformáció az időszak egynegyedét követően maximális lesz, azaz idővel.
6. probléma: Egy tömeges golyó repül sebességgel υ egy 2 m tömegű pihentető golyóra. Keresse meg a két golyó sebességét egy rugalmas központi ütközés után.
A tömegközépponthoz tartozó referenciakeretben a két golyó teljes lendülete nulla az ütközés előtt és után. Könnyű kitalálni, hogy a véges sebességre adott válasz kielégíti mind ezt a feltételt, mind pedig az energiagazdálkodási törvényt: a sebesség ugyanolyan, mint az ütközés előtti, nagyságrendben, de irányát az ellenkező irányba változtatja. A rendszer tömegközéppontjának sebessége. A tömegrendszer közepén az első gömb sebességgel mozog, és a második gömb az első sebesség felé mozog. Az ütközés után a golyók ugyanolyan sebességgel repülnek. Visszatér az eredeti referenciakerethez. A sebességnövelés törvényét alkalmazva megállapíthatjuk, hogy a tömeges golyó véges sebessége egyenlő és visszahúzódik, és a tömeges golyó sebessége korábban megegyezik és előre irányul.
Megjegyezzük, hogy a tömegközéppontban nyilvánvaló, hogy az ütközés hatására a golyók relatív sebessége nem változik nagyságrendben, hanem változik az irányba. És mivel a sebességváltozás nem változik a másik inerciális referenciakeretbe való átmenet során, feltételezhetjük, hogy ezt a fontos kapcsolatot a kiindulási referenciakerethez kaptuk:
ahol a υ betű a kezdeti sebességek kijelölésére szolgál, és u - a végsebességeknél. Ez az egyenlet megoldható a lendület megőrzésének törvényével, az energia megőrzésének törvénye helyett (ahol a sebesség a második hatalomba kerül).
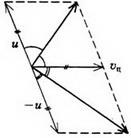
Probléma 7. Ismeretes, hogy két azonos golyó elasztikus nem centrális ütközés esetén, amelyek közül az egyik az ütközés előtt nyugodt volt, a kitágulás szöge 90 °. Igazolja ezt az állítást.
A tömegközéppontban a nem centrális ütközés leírása az alábbiak szerint történik. Mielőtt üti a labdákat jönnek össze az azonos lendület, az ütközés után repülnek az azonos nagyságú, de ellentétes impulzusok és direkt expanziós elfordul egy bizonyos szöget zár be a közvetlen megközelítés. Ahhoz, hogy menjen vissza a kezdeti referenciakeret, szükséges megállapítani minden véges sebesség (vector!) A tömegközéppont sebessége. Abban az esetben, azonos golyókat tömegközéppont sebessége, ahol υ - sebessége bejövő labdát, és a tömegközéppont referenciakeret labdák konvergálnak és szórás egyenlő sebességgel. Az a tény, hogy minden egyes hozzáadása után a végleges sebességét a tömegközéppont sebessége kapott kölcsönösen merőleges vektorok, láthatjuk, a 9. ábra egyszerűen ellenőrizheti, hogy a skalár szorzata vektorok és eltűnik annak a ténynek köszönhető, hogy a modulok a vektorok egyenlő egymással.
1. A m tömeg és az l hosszúságú rúd az egyik végén van csuklósan. A rudat a függőleges helyzetből bizonyos szögben elhajították és felengedték. A függőleges helyzet áthaladásakor az alsó pont sebessége υ. Keresse meg a feszültséget a rúd középpontján ezen a ponton.
2. A m tömeg és az l hosszúságú rudat vízszintes síkban forgatjuk, amelynek szögsebessége az egyik végénél. Keresse meg a rúd feszességét az x távolsággal a forgástengelyhez képest, ha a másik végén kis tömegű, M tömegű.
3. Keresse meg a rezgésperiódust a papír 5. feladatában leírt rendszerhez, de különböző m1 és m2 tömegű rudakhoz.
4. Végezze el a két golyó elasztikus központi hatásának ismert általános képletét, a tömeg-referenciarendszer közepére való átmenet segítségével.
5. Az m1 tömegű golyó egy kisebb tömegű pihentető labdát talál. Keresse meg a baleset labdájának legnagyobb lehetséges szöget egy rugalmas, nem centrális ütközés esetén.