Job Options
a) ((A B) (C A)) (B C);
b) ((((A B) A) B) C) C;
c) (A (B C)) ((A C) (A B)).
2. Az SDNF és az SKNF képletekhez való hozatal:
3. Egy adott változóérték-készlethez hozzon létre egy elemi összefüggést, amely csak a változók értékeinek halmazára igaz.
4. Egy adott változóérték-készlet esetén hozzon létre egy elemi elhatárolást, amely csak a változók ezen értékkészletére érvényes.
5. Konstruáljon SKNF-et és SDNF-et, amely egyenértékű ezzel a képletével, és találja meg azokat a értelmezéseket, amelyekre a képlet igaz és hamis:
6. Az 1. táblázatban definiált g és h függvényekhez keresse meg az SKN- és VOS-formákat és a legegyszerűbb képleteket, amelyek megvalósítják ezeket a funkciókat.
7. Hozzon létre két logikai függvényt, amelyek az alábbi táblázatban foglaltak szerint 1-bites bináris additort terveznek
ahol x1 és x2 az 1. és a 2. summand azonos számjegye; e1 a legkisebb számjegyből álló hordozóegység; e2 - átviteli egység az összeg legmagasabb számjegyéig; az összegzés eredménye.
8. Konstruáljon egy képletet három változóból, ami akkor igaz, ha csak két változó hamis.
9. Formázzunk három változóból álló képletet, amely ugyanazt az értéket veszi fel, mint a változók többségét (kisebbségét).
10. Az U képlet SKNF szerint konstrukció:
a) az U * kettős képlet CDNF-je;
b) az űrlap SKNF U;
c) a U képletnek megfelelő CDNF.
11. Az SDNF szerint a (B) általános képlet U és CDNF jelentése:
a) SNNF és SDNF képletek (U B);
b) az (U B) képlet SNNF és SDNF;
c) SKNF és SDNF (U B).
3. Teljes műveletek
A műveletrendszer teljesnek mondható. ha bármilyen logikai műveletet képviselhet egy képlet fölött .
Mivel minden képletet a csökkentett képlet képvisel, a rendszer 0 => teljes.
A rendszer csökkenti a * értéket. jelölés *. Ha a rendszer * összes műveletei a rendszer felett formulákkal reprezentálhatók . Ha a * befejeződött, akkor a befejeződött.
Az utolsó kijelentés az egyik módja annak, hogy bebizonyítsuk a műveletek rendszerének teljességét - csökkentve egy ismert, teljes rendszerre, például 0-ra. Ez azt jelenti, hogy a rendszer befejeződik, amelynek műveletei során egy összefüggést, egy diszjunkciót és egy negációt fejez ki.
Feladat. Bizonyítsd be a rendszer teljességét 5 =.
A megoldás. A rendszert 5 a teljes 0 rendszerre csökkentjük.
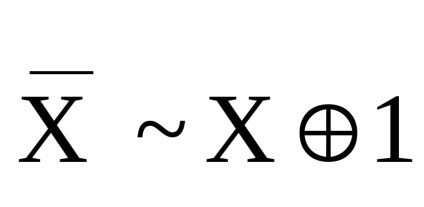
.
Ha egy tetszőleges formula Zhegalkin algebra, felismerve egy f Boole-függvény, nyissa meg a konzolok és tegyen meg minden lehetséges egyszerűsítések, kapunk egy formula, amely formájában a szorzatok összege, azaz a polinom mod 2. Ez a képlet az úgynevezett polinom Zhegalkin ezt a funkciót. Egy lineáris függvényt olyan függvénynek nevezünk, amelynek Zhegalkin-polinomja lineáris.
Feladat. Mutassa be a képletet (x1 x2) (
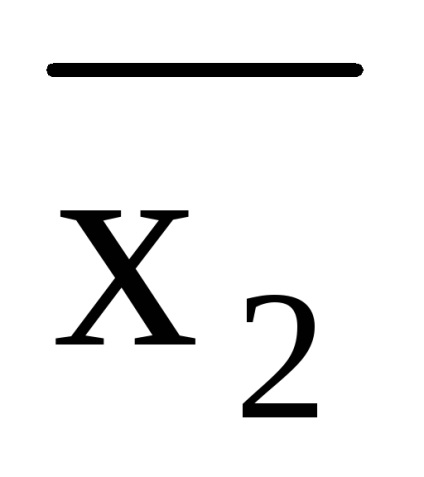
(x1 x2) (
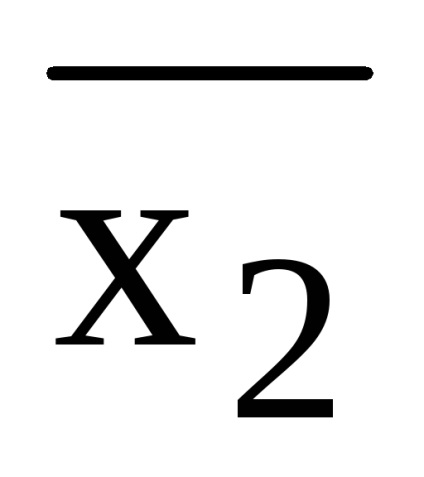
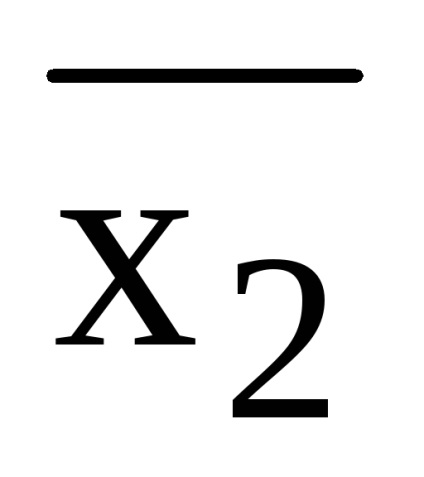
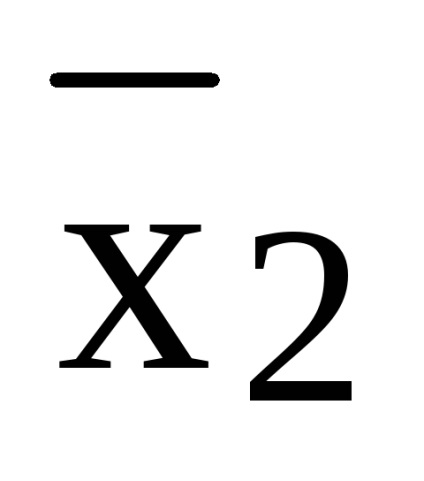
= x1 x2 x3 x1
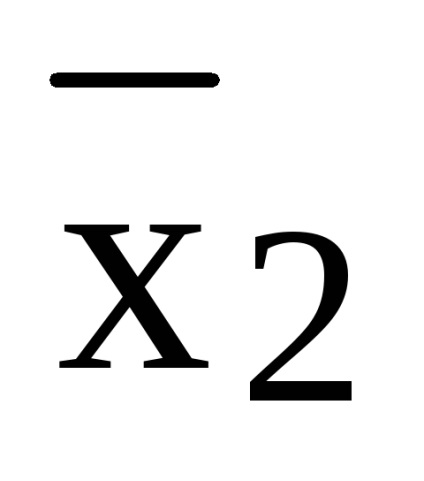
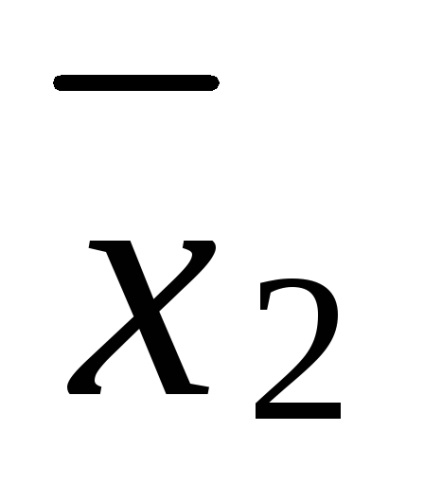
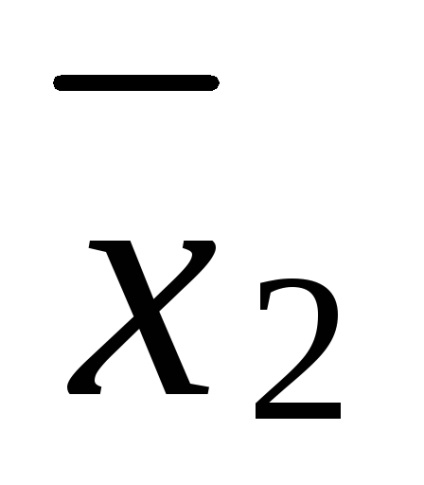
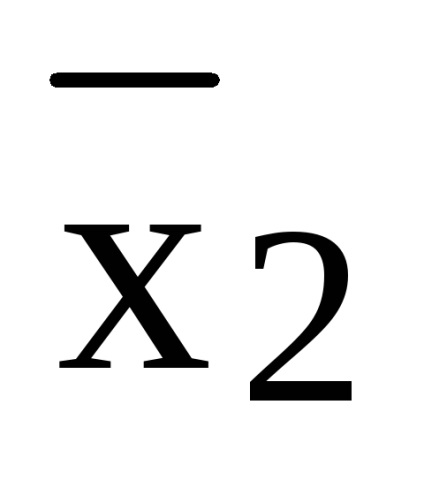
Az eredményül kapott polinom nem lineáris és 3. fokú.
A teljes működési rendszer redukálhatósága szükséges feltétele a működési rendszer teljességének. Az operációs rendszer teljességéhez szükséges és elégséges feltétel a logikai függvények megfogalmazása.
Az F logikai függvények rendszere teljesnek mondható, ha bármelyik függvény megvalósítható egy F képlet fölött.
A Post tétel. Logikai rendszer funkcióinak teljes, ha és csak akkor, ha legalább egy funkció, nem menti 0, legalább egy funkció, nem menti 1 legalább egy nesamodvoystvennuyu funkció, legalább egy nem-monoton függvény és legalább egy nem-lineáris függvény.
Feladat. Bizonyítsa be a rendszer teljességét 0. a szükséges és elégséges teljességi feltétel felhasználásával.
A megoldás. A Boole függvények megfelelő rendszereit F0 =
A funkciók megőrzése 0.
A funkciók megőrzése 1.