Megoldása rendszerek lineáris egyenletek Gauss

Gauss - a klasszikus módszer megoldására egy lineáris algebrai egyenletek (Slough). Tekintsük a lineáris egyenletrendszer állandó együtthatós érvényes:
vagy mátrix formában
Gauss módszer megoldására lineáris egyenletek két lépésből áll:
- szekvenciális (közvetlen) kizárás;
- fordított helyettesítéssel.
következetes kivétel
Gauss elimináció az elképzelésen alapul, szekvenciális változók egy kivételével, ameddig nem lesz egyetlen egyenlet egyetlen változó a bal oldalon. Akkor ez az egyenlet megoldható egyetlen változót. Így, az egyenletrendszert vezet egy háromszög alakú (lépcsős) módon. Ennek az első oszlopban közül kiválasztott nulla mátrix elemek (és gyakran maximum) elemet, és mozgassa azt a legfelső helyzetbe sorban permutáció. Ezután az összes egyenletet normázza elosztjuk azt ai1 együtthatóval. ahol i - az oszlop számát.
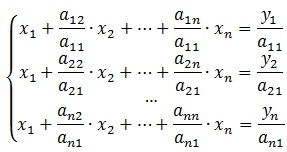
Ezután kivonjuk kapott átrendezése után az első sorban a fennmaradó sorok:
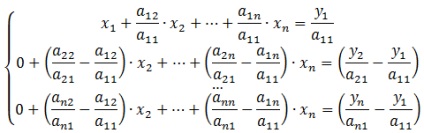
Kap egy sor új egyenletek, amelyek helyébe a megfelelő együtthatók.
Miután ezek az átalakulások volna elérni, az első sorban és első oszlop és mentálisan eltávolítottak tovább az eljárás minden további egyenletek amíg egyenlet egy ismeretlen:
Kapcsolat a helyettesítés
Kapcsolat a helyettesítés során a helyettesítés amelyet az előző lépésben a változó értékét xn az előző egyenlet:
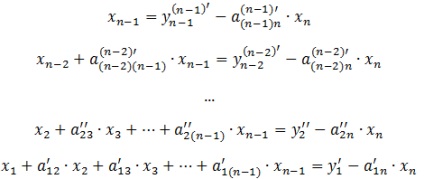
Ezt az eljárást megismételjük az összes többi döntések:
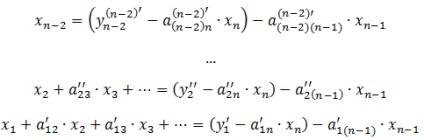
példát szemléltet
Adott egy egyenletrendszert
vagy mátrix formában
Válassza ki a sort a legnagyobb együttható ai1 és módosíthatja az első.
Mi normalizálják az egyenlet együttható x1:
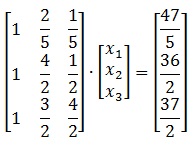
Kivonás 1 egyenletből a 2. és 3:
Kiválasztása egy string a legnagyobb együttható AI2 (1. egyenlet nem tekinthető) és tolja a helyére 2.
Normalizálja a egyenletek 2. és 3. tekintetében együttható x2
Kivonás 2 3. egyenletben
Mi normalizálja a 3. egyenlet képest együttható x3
Hogyan jutunk x3 = 2. Mi helyettesíti a kapott érték az egyenleteket az 1. és 2. megkapjuk
Behelyettesítve ez az érték x2 = 5 egyenletben 1, megkapjuk
Így megoldása az egyenletrendszert a vektor
Megvalósítás C ++
#include
using namespace std;
// megjeleníti az egyenletrendszert
void sysout (dupla ** egy, kettős * y, int n)
A (int i = 0; i
>
cout <<" = " <
return;
>
kettős * Gauss (dupla ** egy, kettős * y, int n)
dupla * x, max;
int k, index;
const dupla EPS = 0,00001; // pontosság
x = új dupla [n];
k = 0;
míg a (k
max = abs (a [K] [k]);
index = k;
A (int i = k + 1; i
max = abs (a [i] [k]);
index = i;
>
>
// sorban permutációs
if (max
cout <<"Решение получить невозможно из-за нулевого столбца " ;
cout <
>
A (int j = 0; j
[K] [j] = a [index] [j];
egy [index] [j] = temp;
>
kettős temp = y [k];
y [k] = y [index];
Y [index] = temp;
// normalizálás egyenletek
A (int i = k; i
if (abs (temp)
Y [i] = y [i] / temp;
ha (i == k) továbbra is; // egyenlet nem kivonni magát
A (int j = 0; j
Y [i] = y [i] - y [k];
>
k ++;
>
// fordított helyettesítéssel
A (k = n - 1; k> = 0; k--)
x [K] = y [k];
A (int i = 0; i
>
vissza x;
>
int main ()
dupla ** egy, * y, * x;
int n;
rendszer ( "CHCP parancs 1251");
rendszer ( "CLS");
cout <<"Введите количество уравнений: " ;
cin >> N;
a = új dupla * [n];
y = új dupla [n];
A (int i = 0; i
A (int j = 0; j
Kapcsolódó cikkek