Szükséges a konvergencia számos
A szükséges feltétele a konvergencia egy szám: A szám csak egyetértenek, ha általános távú hajlamos 0 amint n
Elegendő kritériuma az eltérés a sorozat. Ha az általános kifejezés nem hajlamos 0 => a sorozat elágazik
Vigyázat: szükséges feltétele = 0 nem elegendő a konvergencia a sorozat. Számos melyik. konvergálhatnának vagy eltérhetnek.
1. példa Számos 0,4 + 0,44 + 0,444 + 0,4444 + ...
elágazik, mert általános kifejezés nem hajlamosak 0.
2. példa Számos 1-1 + 1-1 + ...
eltér a = Általános kifejezés nem hajlamos a 0.
És általában nincs határa.
3. példa Több mint elágazik
5) szám + ... + úgynevezett harmonikus sor divergens és a következő, mivel szekvenciáját a részösszegként növekszik a végtelenségig.
Ie a szükséges konvergencia a jel lehetetlenné teszi megítélni, hogy a sorozat konvergál. Konvergencia és divergencia a sorozat sok esetben lehet beállítani elegendő bizonyíték a konvergencia.
Vegyünk néhány közülük znakopolozhitelnyh sorozat, azaz a sorozathoz a nem-negatív értelemben (znakootritsatelny menetek száma itt znakopolozhitelny szorozni (-1), amely nem befolyásolja a konvergencia a sorozat).
Elegendő bizonyíték a konvergencia
sorozat relációs jel
Konvergencia vagy divergencia egy sor znakopolozhitelnogo gyakran alakult összehasonlítva másokkal ( „referencia”) adott, amelyről ismert, hogy közelednek, vagy sem.
„Referencia” gyakran a sorok:
a) a harmonikus sor - eltérő, vagy
b) egy mértani :.
· Ha a sorozat konvergál
· Ha a sorozat eltér
· Ha a sorozat eltér
Ez felírható a következőképpen:
=> Ez a szám exponenciálisan, ahol a =
q = => a sorozat konvergál.
Tétel. Két znakopolozhitelnyh sorozat Tegyük fel, hogy
Ha az egyenlőtlen n => a konvergenciája a második sorban kell konvergenciája az első sorban, az első sor a divergencia következik egy második sorozatát divergencia.
1) Annak vizsgálatára, a konvergencia sorozat
Vessük össze ezt a számot, számos
mértani sorozat érdekében, amely konvergens, mint q =
mert => A sorozat konvergál.
2) Annak vizsgálatára, a konvergencia a sorozat:
Vessük össze ezt a számot a harmonikus sor:
1+ divergens sor annak érdekében,
mert Minden => a sorozatból elágazik
3) Annak vizsgálatára, a konvergencia sorozat
Összehasonlítható számos mértani:
. amely konvergál (q =
mert => A sorozat konvergál
4) A konvergencia a sorozat: 1+
Összehasonlítás egy sor exponenciálisan
Tétel: Adott egy számot znakopolozhitelny + ... és van egy véges vagy végtelen határ
Ezután a sorozatot konvergál <1; и расходится при>1
(Ha = 1, a konvergencia megoldatlan marad)
(D'Alembert-féle vizsgálat indokolt alkalmazni, ha az általános kifejezés a sorozat tartalmaz n! Or)
1) Annak vizsgálatára, a konvergencia sorozat
= => L = 0<1 =>ez a sorozat konvergál alapján a d'Alembert.
L = 3> 1 => szám alapján a D'Alembert divergál.
Cauchy attribútum (gyökös)
Mivel számos
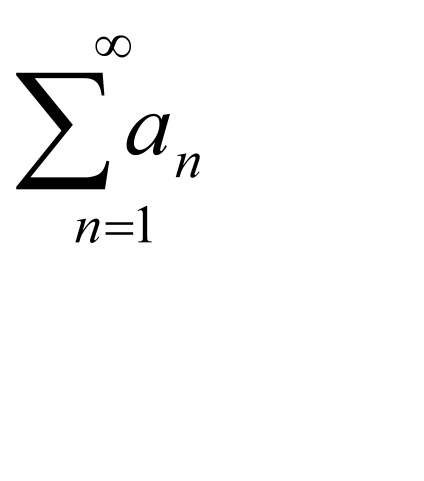
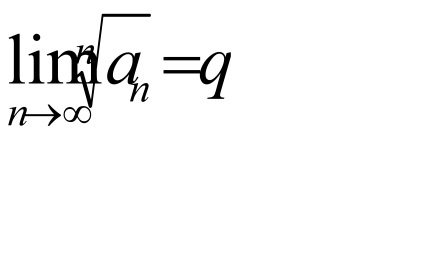
Ha q> 1, akkor a sorozatot divergál.
Ha q<1, то ряд сходится.
Leibniz-jel (a váltakozó sorozat):
A sorozat konvergens, ha két feltétel teljesül:
1) elemek száma nagyságrendű monoton csökkenő;
2) korlátozzák az általános kifejezés a sorozat nulla.
Teljesítmény sorozat egy sor formájában
Ahhoz, hogy megtalálja hatványsorba intervallumban konvergencia szükséges:
1) d'Alembert tesztet kell alkalmazni a sorban vagy a Cauchy összeállított modulok;
2) megvizsgálja a konvergencia a sorozat a végén az intervallum.
Példa 1.Issledovat a konvergencia tartományban
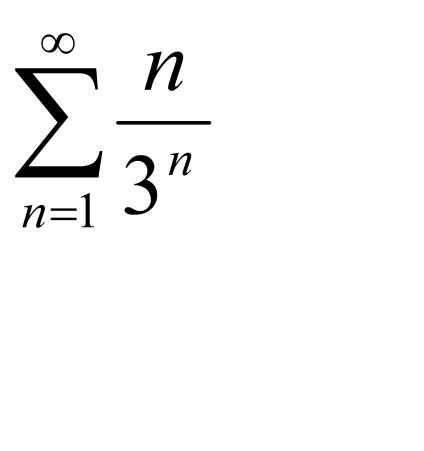
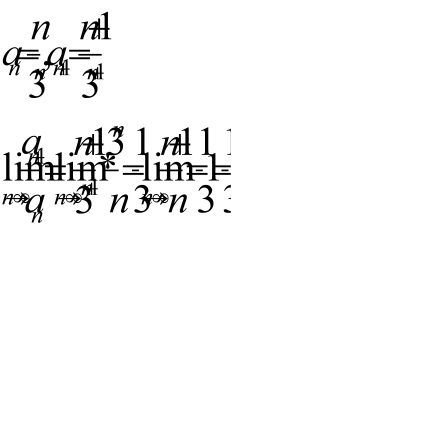
T. k.
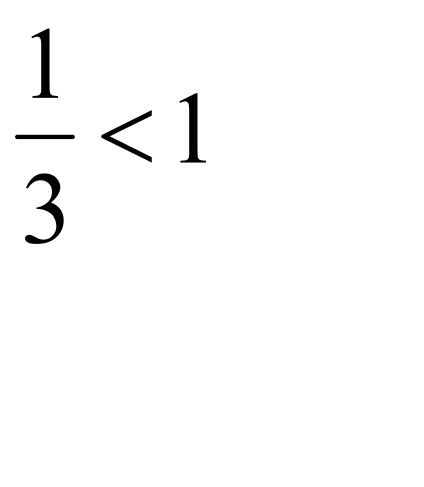
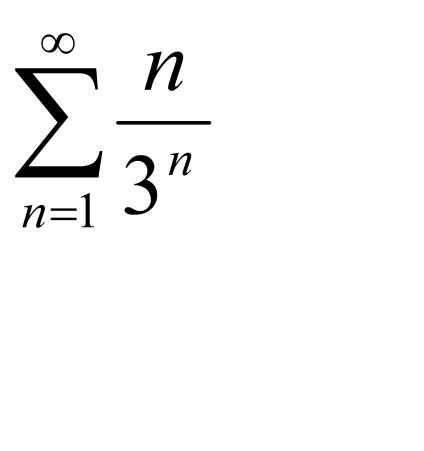
konvergál alapján a d'Alembert.
2. példa. Fedezze fel a konvergencia a sorozat
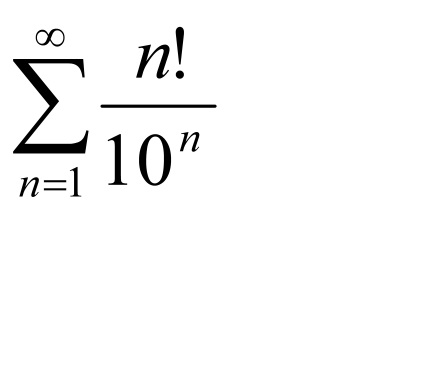
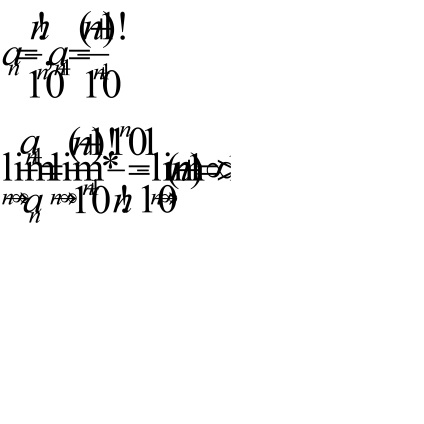
T. k.
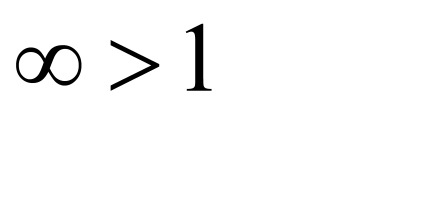
3. példa Vizsgálati konvergencia tartományban

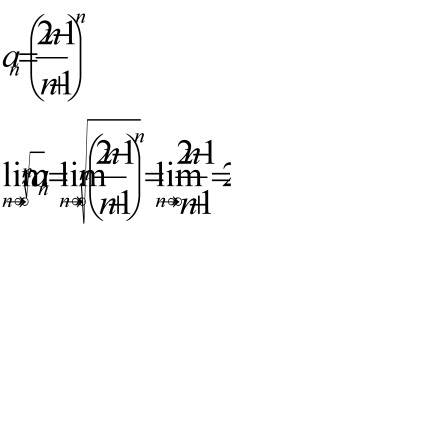
mert
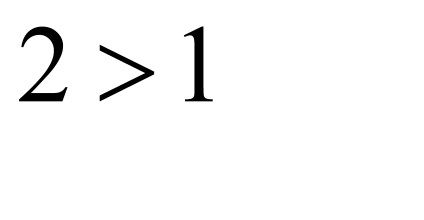
4. példa a megjelölés használata Leibniz megvizsgálta a konvergencia tartományban
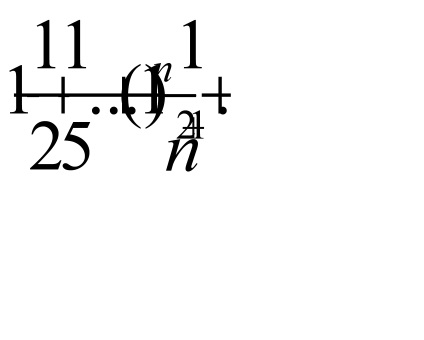
Mivel a tagok a sorozat abszolút értékben monoton
csökkenés
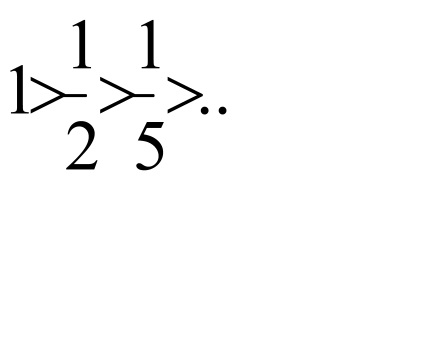
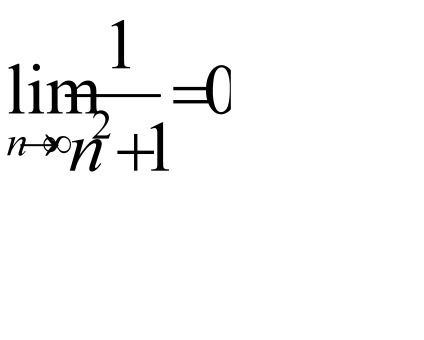
Példa 5.Issledovat az abszolút és feltételes konvergencia sorozat:
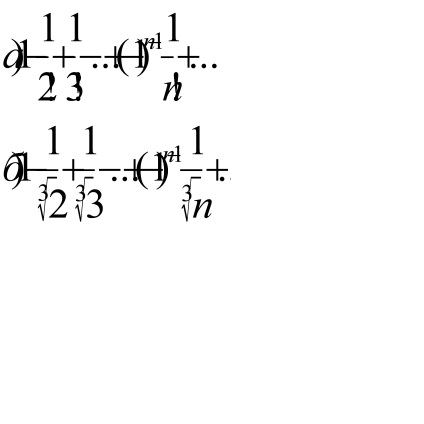
a) Tekintsük a sorozat, amely az abszolút értékek
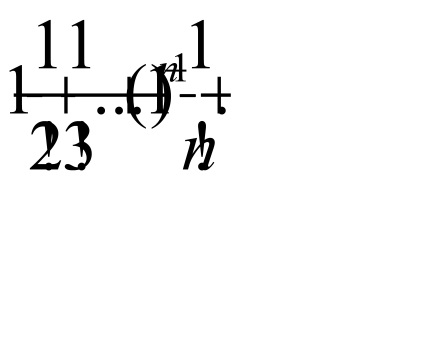
Alapján a d'Alembert sorozatból konvergál, hiszen

Így a sorozat eltér teljesen.
b) álló számot abszolút értékeinek a feltételeket a sorozat
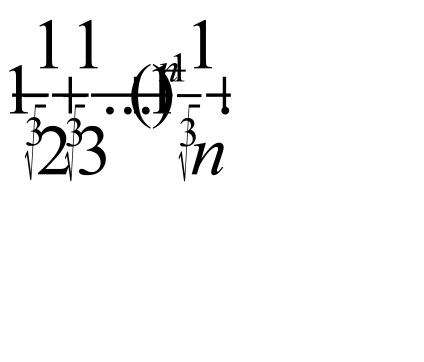
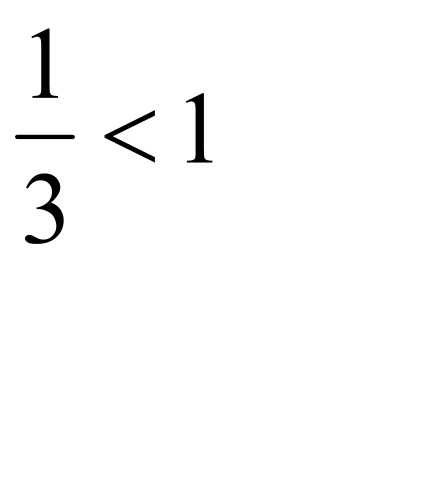
Ennek megfelelően az eredeti sorozat nem abszolút konvergens.
Megvizsgáljuk neki feltételes konvergencia.
sor
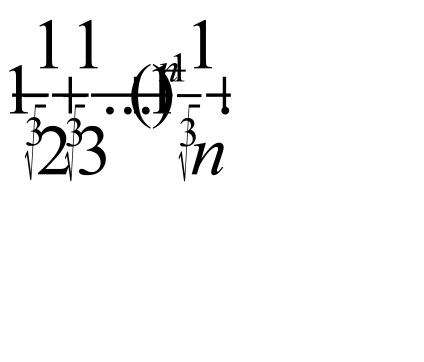
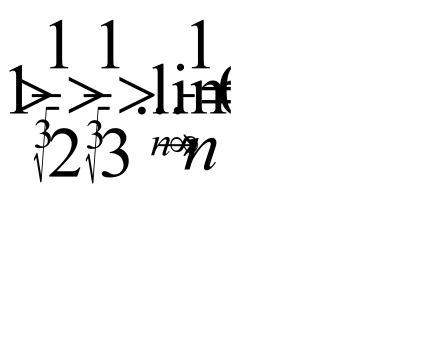
Tehát a sorozat konvergál feltételesen.
6. példa Keresse a domain konvergencia hatványsorba
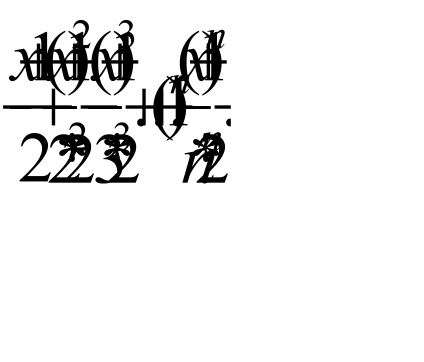
Tekintsük a sorozat, amely az abszolút értékek
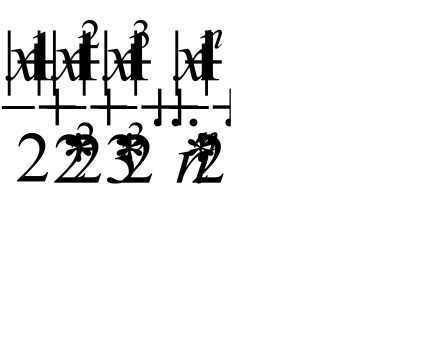
Alapján a d'Alembert

Tekintsük az egyenlőtlenség
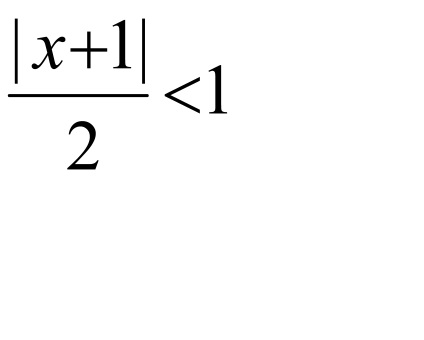
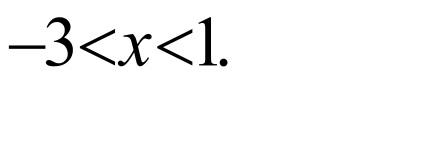
Megvizsgáljuk a konvergencia a végén a különbség.
Amikor x = -3 megkapjuk a sorozat:
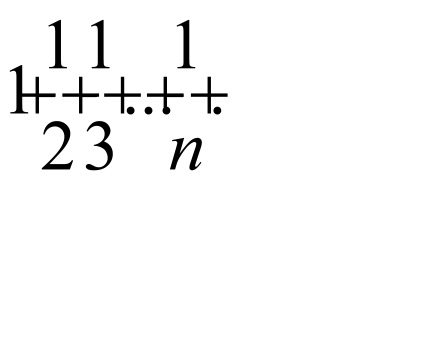
Amikor x = -3 megkapjuk a sorozat:
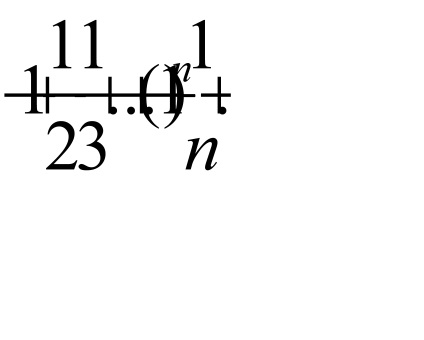
Így az intervallum a konvergencia a sorozat egy rés
Fedezze fel a konvergencia a sorozat: