Konfiguráció (geometria)
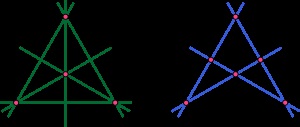
A projektív geometriában egy síkbeli konfiguráció egy véges pontkészletből és egy véges vonal-konfigurációból áll. oly módon, hogy minden egyes pont néhány sorra esik, és minden egyes vonal bizonyos számú pontra esik [2].
Bár néhány konkrét konfigurációkat korábban tanulmányozták (pl Thomas Kirkmanom [en] 1849-ben), a hivatalos vizsgálat konfigurációk először kezdett Theodor Reye [en] 1876-ban a második kiadása könyvében Geometrie der Lage (geometria helyzete) keretében a vita a tétel a Desargues. Ernst Steinitz írt disszertációt a témában 1894-ben és konfigurációk voltak polulyarizirovany 1932 Hilbert és Cohn-Vossenom könyv Anschauliche Geometrie (geometria és), amely később lefordították angol [3].
Konfigurációk lehet tanulmányozni akár a konkrét pontok és vonalak egy adott geometria, mint az euklideszi vagy projektív sík (ebben az esetben az egyik beszél, a végrehajtás geometria), vagy mint egy absztrakt geometriai előfordulása. Az utóbbi esetben, a konfigurációs szoros kapcsolatban rendszeres hipergráfokra és biregular [en] páros gráfban. de a további megszorítás - bármely két pont beesési szerkezetek társítható legnagyobb egyszeri tétel, és bármely két vonal társítható egyetlen maximális pontot. Vagyis a megfelelő kétpárti grafikon (Lévy konfigurációs gráf) körvonala legyen legalább hat.
A síkban lévő konfigurációt (pγℓπ) jelöli, ahol p a pontok száma, ℓ a vonalak száma, γ az egyes pontokon áthaladó vonalak száma, π pedig az egyes sorokban lévő pontok száma. Ezeket a számokat, kapcsolatot
mivel ez a termék egyenlő a pont-on-line incidensek számával (zászlók).
Az azonos szimbólummal rendelkező konfigurációk nem feltétlenül izomorfak, mint előfordulási minták. Például három különböző konfiguráció létezik (93 93) - a Papp konfiguráció és két kevésbé észrevehető konfiguráció.
Bizonyos konfigurációkban p = ℓ és ezért γ = π. Ezeket szimmetrikus vagy kiegyensúlyozott [4] konfigurációknak nevezzük, és általában a jelölésben az ismétlést el kell hagyni. Például (93 93) csökken (93).
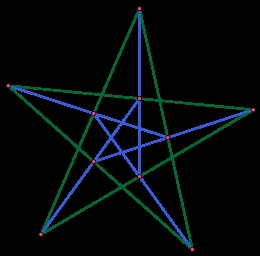
A konfiguráció (103), amely nem izomorf a Desargues-konfiguráció előfordulásával kapcsolatban
A következő projektív konfigurációk a leginkább észlelhetők:
- (11), a legegyszerűbb konfiguráció, amely egy egyenes vonalból áll. A trivialitás miatt gyakran nem veszik figyelembe.
- (32), egy háromszög. Mindhárom oldal a két csúcs közül kettőt tartalmaz, és fordítva. Általában minden n-oldalú poligon egy (n2) típusú konfigurációt alkot,
- (43 62) és (62 43), egy teljes négyszög és egy teljes négyszög [1].
- (73), a Fano sík. Ez a konfiguráció az incidencia absztrakt geometriájaként létezik. De nem lehet az euklideszi síkon építeni.
- (83), a Mobius-Cantor konfiguráció. Ez a konfiguráció két, egymással egyidejűleg leírt és beillesztett négyszögből áll. A konfiguráció nem építhető fel az euklideszi síkon, de az egyenleteket meghatározó komplex számok nem triviális megoldások.
- (93), a Papp konfiguráció.
- (94 123), Hesse konfigurációja kilenc pontnyi inflexiós tömbön a komplex projektív síkon és tizenkét egyenes vonalon, amelyek mindegyike három pontot tartalmaz. Ez a konfiguráció ugyanazokkal a tulajdonságokkal rendelkezik, mint a Fano sík, nevezetesen, hogy minden olyan vonalat tartalmaz, amely a konfiguráció két pontján áthalad. Az ilyen tulajdonságokkal rendelkező konfigurációk Sylvester-Gallai konfigurációnak nevezhetők. Ezeket a konfigurációkat Sylvester tétele szerint nem létezik valós értékű koordináták [5].
- (103), a Desargues konfigurációját.
- (125 302), a dupla hat Schlafli. 12 egyenes, 27 egyenes köbös felületből áll [en]
- (153), a Cremona - Richmond konfigurációja. A hat egyenes és a 15 érintő síkban nem szereplő 15 egyenes vonal
- (124 163), a Reye konfigurációval.
- (166), a Kummer konfiguráció [en].
- (273), a szürke konfigurációban
- (6015), a Klein konfigurációját [en].
A (pγlπ) projektív kettős konfiguráció egy konfiguráció (lπpγ), amelyben a "pontok" és a "sorok" szerepét egymással kicserélik. Ezért a konfigurációk kettős párok, kivéve, ha a kettős konfiguráció izomorf az eredeti változathoz képest. Ezeket a kivételeket önkommunális konfigurációnak nevezzük, és ebben az esetben p = l [6].
A (n3) típusú nem-inomorf konfigurációk száma, az n = 7-gyel kezdve, a szekvenciát alkotják
Ezeket a számokat absztrakt előfordulási mintákként számítják ki, függetlenül attól, hogy megvalósultak-e [7]. Amint Gropp írja [8]. tízből kilenc konfigurációk (103), és az összes a konfigurációk (113) és (123) lehetővé teszi végrehajtását az euklideszi térben, de minden n ≥ 16 legalább egy konfigurációs megvalósíthatatlan (n3). Gropp azt is jelzi, egy régóta fennálló hiba szekvencia - egy cikket 1895-ben volt, egy kísérlet felsorolni minden konfiguráció (123), és 228 közülük találtak, de a 229-edik konfigurációját nem nyitotta 1988-ig.
Szimmetrikus konfigurációk kialakítása
Számos módszer létezik a konfigurációk megalkotására, általában a már ismert konfigurációktól kezdve. Ezek közül a módszerek közül a legegyszerűbbek szimmetrikus (pγ) konfigurációt hoznak létre.
Az n sorrendű véges projektív sík konfigurációja ((n 2 + n + 1) n + 1). Legyen Π egy projektív tervezési sík n. Eltávolítjuk a P pontot az Π-ből és a P-en átmenő összes vonalat (de nem a ponton fekvő pontokat, kivéve a P pontot), és eltávolítjuk az l vonalat. nem áthaladva a P. és az összes ponton fekszik ezen a vonalon. Ennek eredményeként létrejöhet a ((n 2 - 1) n) típusú konfiguráció. Ha az l vonalat választjuk az építményben. a P-n áthaladva a ((n 2) n) típusú konfigurációt kapjuk. Mivel ismeretes, hogy minden n. Sorrendben léteznek projektív síkok. amelyek primitívek, ezek a konstrukciók végtelen számú szimmetrikus konfigurációval rendelkeznek.
Nem minden konfiguráció valósítható meg, például a konfiguráció (437) nem létezik [9]. Azonban Csoport [10] adott egy szerkezet, mely azt mutatja, hogy k ≥ 3 konfiguráció (pk) létezik minden p ≥ 2 lk + 1, ahol LK a hossza az optimális Golomb vonalzók rendelni k.
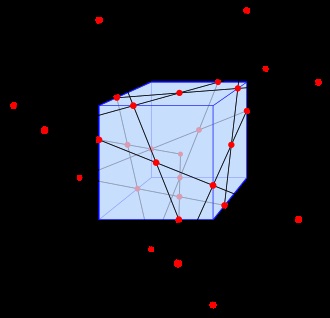
A konfiguráció koncepciója általánosítható a nagyobb dimenziókra, például pontokra, vonalakra vagy síkokra. Ebben az esetben gyengíthetjük azt a korlátozást, hogy két pont nem fekszik több mint két sorban, mivel két pont egynél több síkhoz tartozhat.
A háromdimenziós térben,
- Mobius konfiguráció. két egymásba írt tetraéderből áll
- Reye konfiguráció. amely tizenkét pontból és tizenkét síkból áll, hat ponttal minden síkon és hat síkon, amelyek minden ponton áthaladnak
- Szürke konfiguráció. amely 27 rácspontból áll, 3 × 3 × 3 és 27 ortogonális vonalból
- A dupla hat Shlefli. 30 pontból és 12 egyenesből, két egyenes egy pontból és öt pontból egy egyenes vonalból áll.
További dimenziót nyerünk háromdimenziós térben, amikor figyelembe vesszük a pontok, vonalak és síkok előfordulását, vagyis a j-szóközöket 0 ≤ j <3, где каждое j -пространство инцидентно Njkk -пространствам (j ≠ k ). Если обозначить через Njj число j -пространств, такую конфигурацию можно представить в виде матрицы :
A megközelítés általánosítható más n. ahol 0 ≤ j
Kapcsolódó cikkek