Teljesítményfunkció, tulajdonságok, grafikonok, algebra, 11 óra, lecke és bemutató
Teljesítményfüggvények, definíciós tartomány.
Srácok, az utolsó leckében tanultuk meg, hogyan kell számokkal dolgozni egy racionális exponenssel. Ebben a leckében fontolóra veszi a hatalom funkcióit, és arra korlátozódik, hogy az exponens racionális.
Figyelembe vesszük az űrlap funkcióit: $ y = x ^> $.
Először a $ \ frac> 1 $ expozíciót vizsgáljuk.
Tegyük fel, hogy egy adott $ y = x ^ 2 * 5 $ függvényt kapunk.
Az utolsó leckében megadott definíció szerint: $ x≥0 $, akkor a függvénydefiníciónk tartománya $ [0; + ∞) $.
Az értékek táblázata.
Hagyjuk át az esetet, ha a kitevő megfelelő frakció (azaz ha a számláló kisebb, mint a nevező).
Összehasonlítsuk a három teljesítményfunkciót: $ y = x ^ 2 $; $ y = x ^ $; $ y = x ^ 3 $.
A 2,5-es szám 2 és 3 közé esik, aztán úgy tűnik, hogy függvényünk grafikonja is a megfelelő grafikonok között helyezkedik el. Összehasonlítjuk a függvények értékeit a különböző x értékekkel.
1. Ha $ 0
Az első ábrán grafikonokat készítünk a $ 0 esetreA teljesítményfunkciók tulajdonságai
A függvény tulajdonságai $ y = x ^> $, $ (m> n) $:
1. $ D (y) = [0; + ∞) $.
2. Sem sem vagy furcsa.
3. $ [0; + ∞) $ értékkel növekszik.
4. A fentiek nem korlátozottak, az alábbiakban korlátozottak.
5. Nincs legnagyobb érték, a legkisebb érték nulla.
6. folyamatos.
7. $ E (f) = [0; + ∞) $.
8. Hajtson le.
A $ y = x ^> $, $ (m> n) $ függvény grafikonja hasonló a $ y = \ sqrt [n] $ függvény grafikonjához. Vázoljunk le függvénygrafikont. 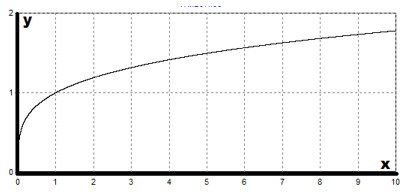
A $ y = x ^> $, $ 0 0 $ függvény tulajdonságai és r minden racionális szám, akkor a $ y = x ^ r $ teljesítményfüggvény deriváltja a következő képlet segítségével számítható ki: $ y '= r * x ^ $.
Egy példa. Keresse meg a $ y = x ^> $ függvény legnagyobb és legkisebb értékét az intervallumon:
a) $ [1; 16] $,
b) $ (2,10) $,
c) a sugáron $ [9; + ∞) $.
A megoldás.
A funkció kitevője pozitív. Ezután a funkciónk tulajdonságait vizsgálva látjuk, hogy a meghatározás teljes területén nő. Ez azt jelenti, hogy az adott szegmensek végein eléri a legnagyobb és a legkisebb értékét (ha ezeken a pontokon van meghatározva).
a) $ y_ = 1 ^> = 1 $; $ y_ = 16 ^> = (\ sqrt) ^ 5 = 4 ^ 5 = 1024 $.
b) A funkció ezen a tartományon belül nincs a legnagyobb és legkisebb érték, mivel nyitott intervallumot kapunk, és a 0 és 4 pontok nem tartoznak ebbe az intervallumhoz.
c) A legnagyobb érték nem.
$ y_ = 9 ^> = \ sqrt = (\ sqrt) ^ 5 = 3 ^ 5 = 243 $.
Egy példa. Keresse meg a függvény legnagyobb és legkisebb értékét: $ y = \ fracx ^> - \ fracx ^ 4 $ az $ [1; 9] $ tartományban.
A megoldás.
Srácok, emlékszel, hogyan találtuk a funkció legnagyobb és legkisebb értékét a 10. fokozatú szegmensben?
Igaz, egy származékot használtunk. Oldjuk meg a példát, és ismételjük meg az algoritmust a legkisebb és legnagyobb érték megállapításához.
1. Lássuk egy adott függvény származékát:
$ y '= \ frac * \ fracx ^> - x ^ 3 = 8x ^> - x ^ 3 = 8 \ sqrt-x ^ 3 $.
2. A származék a kezdeti függvény definíciójának teljes területén létezik, akkor nincsenek kritikus pontok. Találjuk meg az álló pontokat:
$ y '= 8 \ sqrt-x ^ 3 = 0 $.
$ 8 * \ sqrt = x ^ 3 $.
$ 64x ^ 3 = x ^ 6 $.
$ x ^ 6-64x ^ 3 = 0 $.
$ x ^ 3 (x ^ 3-64) = 0 $.
$ x_1 = 0 $ és $ x_2 = \ sqrt [3] = 4 $.
Az adott szegmens csak egy megoldást tartalmaz $ x_2 = 4 $.
A szegmens végein és a végső pontján egy függvénytábla-táblát készítünk:
A válasz: $ y _ = - $ 862.65 $ for $ x = 9 $; $ y_ = 38,4 $ a $ x = 4 $ -hoz.
Egy példa. Oldja meg az egyenletet: $ x ^> = 24-x $.
A megoldás. A $ y = x ^> $ függvény grafikonja növekszik, és a $ y = 24-x $ függvény grafikonja csökken. Srácok, tudjuk, hogy ha egy függvény növekszik, és a másik csökken, akkor csak egy ponton metszik egymást, vagyis csak egy megoldásunk van.
Megjegyzés:
$ 8 ^> = \ sqrt [3] = (\ sqrt [3]) ^ 4 = 2 ^ 4 = 16 $.
$ 24-8 = $ 16.
Vagyis $ x = 8 $ esetén a megfelelő egyenlőség $ 16 = 16 $, ez az egyenlet megoldása.
A válasz $ x = 8 $.
Egy példa.
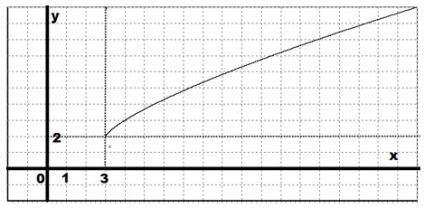
Konstruáljon egy függvény grafikont: $ y = (x-3) ^ \ frac + 2 $.
A megoldás.
A funkció grafikáját a $ y = x ^> $ függvény grafikonjából kapjuk meg, 3 egység jobbra és 2 egység felfelé mozgatásával.
Egy példa. Írja az érintő egyenletét a $ y = x ^> $ sorba a $ x = 1 $ pontban.
A megoldás. Az érintő egyenletét az általunk ismert képlet határozza meg:
$ y = f (a) + f '(a) (x-a) $.
A mi esetünkben $ a = 1 $.
$ f (a) = f (1) = 1 ^> = 1 $.
Találjuk meg a származékot:
$ y '= - \ fracx ^> $.
Számolunk:
$ f '(a) = - \ frac * 1 ^> = - \ frac $.
Lássuk az érintő egyenletét:
$ y = 1 \ frac (x-1) = - \ fracx + 1 \ frac $.
A válasz: $ y = - \ fracx + 1 \ frac $.
A független megoldások feladatai
1. Keresse meg a függvény legnagyobb és legkisebb értékét: $ y = x ^ \ frac $ a szegmensben:
a) $ [1; 8] $.
b) $ (4,50) $.
c) a sugáron $ [27; + ∞) $.
2. Keresse meg a $ y = \ fracx ^> - x $ függvény legnagyobb és legkisebb értékét az $ [1; 27] $ tartományban.
3. Oldja meg az egyenletet: $ x ^> = 18-x $.
4. Legyen egy függvény grafikonja: $ y = (x + 1) ^> - 1 $.
5. Írja az érintő egyenletét a $ y = x ^> $ sorba a $ x = 1 $ pontban.