Modellezés a villamosenergia-iparban - numerikus módszerek nemlineáris egyenletek megoldására
Numerikus módszerek nemlineáris egyenletek megoldására. Az akkordok módszere.
Az akkordok módszere (ez a módszer a szekantumok módszerének is ismert) egyike a nemlineáris egyenletek megoldásának, és az egyenlet egy gyökereit tartalmazó intervallum egymást követő szűkülésén alapul. Az iteratív folyamatot a meghatározott pontosság eléréséig végezzük.
A félosztásos módszerrel ellentétben az akkord módszer azt sugallja, hogy a megfontolt intervallum megosztása nem a középső, hanem az akkord metszéspontjával történik az abszcisszal (ax-tengely) tengelyével. Meg kell jegyezni, hogy az akkord olyan szegmens, amelyet a függvény pontjai a vizsgált intervallum végein rajzolnak át. Ez a módszer gyorsabb gyökeres eredményt ad, mint a félosztásos módszer, feltéve, hogy ugyanazt az intervallumot vesszük figyelembe.
Geometriailag az akkord módszer egyenértékű azzal, hogy a görbét az u pontokon áthaladó akkordon helyettesíti (lásd az 1. ábrát).
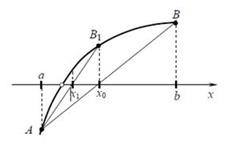
1. ábra. Egy szegmens (akkord) létrehozása egy függvényhez.
Az A és B pontokon áthaladó egyenes (akkord) egyenlete a következő alakú:
Ez az egyenlet egy tipikus egyenlet a közvetlen Descartes-koordinátarendszer leírásához. A görbe meredeksége a koordinátával és az abszcisszal van megadva a denominátorban és a. volt.
A vonal metszéspontja az abszcisszák tengelyével a fent írt egyenlet átíródik a következő formában:
Új iterációs folyamatként válassza ki a két vagy a egyiket. amelynek végein a funkció különböző jelek értékét veszi fel. A szegmens végein a funkció értékeinek ellentétes értelmezése számos módon meghatározható. E módszerek egyike a szekvencia végén lévő függvények értékének szorzása és a termék jeleinek meghatározása a szorzás nullával történő összehasonlításával:
A gyökér finomításának iteratív folyamata, amikor a két egymást követő közelítés közelségének állapota kisebb lesz, mint a meghatározott pontosság, azaz
.
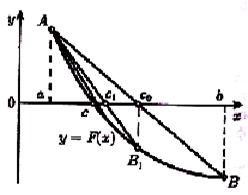
2. ábra. Magyarázat a számítási hiba meghatározására.
Meg kell jegyezni, hogy az akkordok konvergenciája lineáris, de gyorsabb, mint a félosztásos módszer konvergenciája.
Algoritmus egy nemlineáris egyenlet gyökereinek megtalálására az akkordok módszerével
1. Keresse meg a bizonytalanság kezdeti szakaszát a gyökerek elválasztásának egyik módszerével. Állítsa be a számítási hibát (egy kis pozitív számot) és az iteráció () kezdeti lépését.
2. Keresse meg az akkord metszéspontját az abszcisszal:
3. Meg kell találni a funkció értékét a pontokon. és. Ezután két feltételt kell ellenőriznie:
- ha a feltétel teljesül. akkor a kívánt gyökér a bal oldali szegmensben található. ;
- ha a feltétel teljesül. akkor a kívánt gyökér a jobb oldali szegmens belsejében van. .
Ennek eredményeként létrejön egy új bizonytalansági intervallum, amelyen az egyenlet kívánt gyökere található:
4. Ellenőrizzük az egyenlet gyökérének hozzávetőleges értékét egy adott pontosság esetén, a következő esetekben:
- Ha a két egymást követő közelítés különbsége kisebb lesz, mint a megadott pontosság. akkor az iterációs folyamat véget ér. A gyökér hozzávetőleges értékét a következő képlet határozza meg:
- Ha a két egymást követő közelítés különbsége nem éri el a szükséges pontosságot. akkor folytatni kell az iteratív folyamatot, és folytatni kell a vizsgált algoritmus 2. lépését.
Példaként tekintse meg a nemlineáris egyenlet megoldását az akkord módszerrel. A gyökeret a vizsgált tartományban a pontossággal kell megtalálni.
A nemlineáris egyenlet megoldása a MathCAD szoftvercsomagban.

A számítások eredményeit, nevezetesen a gyökér hozzávetőleges értékének változását, valamint az iterációs lépésből származó számítási hibákat grafikus formában adják meg (lásd 1. ábra).
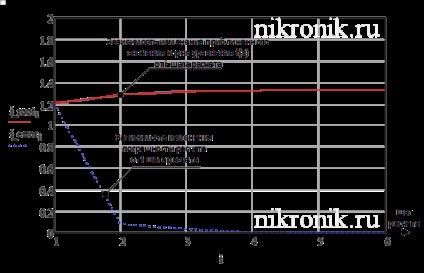
1. ábra. A számítás eredményei az akkordok módszerével
Annak érdekében, hogy a megadott pontosságot a tartományban lévő egyenletre keressük, 6 iterációt kell végrehajtani. Az iteráció utolsó lépésében a nemlineáris egyenlet gyökér hozzávetőleges értékét az alábbi érték határozza meg:.
Ennek a módszernek a módosítása a hamis pozíció (False Position Method) módja, amely csak abban különbözik a secant módszertől, hogy minden alkalommal, amikor az utolsó két pontot veszik, és azokat a pontokat, amelyek a gyökér körül vannak.
Meg kell jegyeznünk, hogy ha a keresési algoritmus második deriváltja leegyszerűsíthető egy nemlineáris függvényből. Tegyük fel, hogy a második származék állandó jelet tartalmaz, és két esetet vizsgál:
Az első feltételből kiderül, hogy a szegmens fix oldala az a oldal.
A második feltételből kiderül, hogy a szegmens fix oldala az oldal b.
Általában a rögzített végpont azonosításához a következő feltételt írhatjuk :. hol vagy.
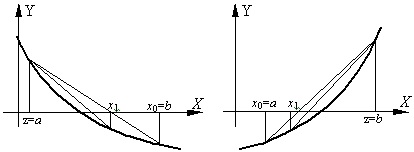
Ábra. 3. Példák egy csökkenő vagy növekvő funkcióra
Így a funkció típusától függően két kifejezést kapunk, hogy egyszerűsítsük a függvény gyökerének keresését:
- ha a függvény megfelel az első esetnek (lásd a 3. ábrát), akkor a képletnek a következő alakja lesz:
- ha a függvény megfelel a második esetnek (lásd a 3. ábrát), akkor a képletnek a következő alakja lesz:
Az ügy a vizsgált esetre csökken. ha az egyenlet formája :.