A valós számok hozzávetőleges értékei
A valós számok hozzávetőleges értékei
A 7. és a 8. osztályban gyakran egyenletesen oldottuk meg az egyenleteket. Észrevetted, hogy szinte minden ilyen példában az egyenletek "jó" gyökerei vannak? Ezek egész számok voltak, amelyek könnyen megtalálhatók grafikonok segítségével, különösen a kockás papírra. De ez nem mindig így van, de még mindig "jó" példákat választottak.
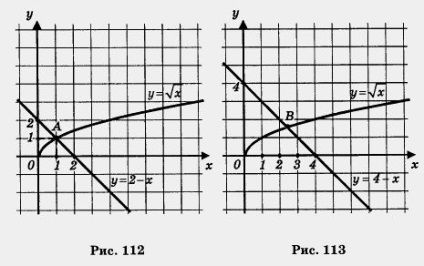
Tekintsünk két egyenletet: = 2 - x és = 4 - x. Az első egyenlet van egy egyedi gyökér x = 1, mert a grafikus funkciók y = 2 és y = - x metszik egy pontján egy (1: 1) (112.). A második esetben a függvények - fc és y = 4 - x grafikonjai egy B pontban (113. Ábra) metszenek, de "rossz" koordinátákkal. A rajz segítségével megállapíthatjuk, hogy a B pont abszcissza megközelítőleg 2,5. Ilyen esetekben nem a pontos megoldásról, hanem az egyenlet közelítő megoldásáról beszélünk, és ezt írjuk:
Ez az egyik oka annak, hogy a matematikusok úgy döntöttek, hogy bevezetik egy valós érték közelítő értékének fogalmát. Van egy másik oka is, és talán még fontosabb: mi a valóságos szám? Ez egy végtelen tizedes tört. De a számítások végtelen decimális frakciókkal kényelmetlenek, ezért a gyakorlatban a valós számok hozzávetőleges értékeit használjuk. Például egy számhoz használja a hozzávetõleges egyenlõséget 3.141 vagy 3.142. Az első az n szám megközelítő értéke (vagy közelítése) egy hibával 0,001 pontossággal; A második a k számának hozzávetőleges értéke (közelítése) a többlet felett a 0,001-es értékig. Pontosabb approximációk lehetségesek: például 3.1415 - közelítés egy hibával 0,0001 pontossággal; 3.1416 - a felesleges közelítés 0,0001 pontossággal. Elmondhatjuk a kevésbé pontos közelítést, például 0,01 pontossággal: 3,14 hiány esetén a 3,15 fölött.
A hozzávetőleges egyenlőség jele ", amelyet az 5-6. És a valószínűleg a fizika tanfolyam matematikája során alkalmaztál, és ezt már korábban használtuk, például a 27. §-ban.
1. példa A hiányosság és a felesleg hozzávetőleges értékeinek meghatározása a számok 0,01 pontosságával:
a) Tudjuk, hogy = 2.236. (lásd a 27. §-t), így a 2.23 egy megközelítés egy hibával, amelynek pontossága 0,01; A 2.24 egy közelítő érték, ami meghaladja a 0,01 pontosságot.
b) 2 + = 2.000. + 2.236. = 4,236. Ezért a 2 + 4.23 egy megközelítés egy hibával, amelynek pontossága 0,01; 2 + 4,24 a 0,01 pontosságú felesleges közelítés.
c) 0,31818. (lásd a 26. fejezetet). Így a 0.31 egy közelítés egy hibával, amelynek pontossága 0,01; A 0,32 érték a 0,01 pontossággal meghaladó közelítés.
A hiányhoz való közelítést és a felesleggel való közelítést néha természetes számoknak hívják.
Definíció. A közelítési hiba (abszolút hiba) az x pontos értéke és a hozzávetõleges értéke közötti különbség modulusa: a közelítési hiba | x - a |.
Például a hozzávetõleges egyenlõség hibáját a vagy,
Pusztán gyakorlati kérdés merül fel: mi a legjobb közelítés, a hiány vagy a felesleg esetén, vagyis abban az esetben, ha a hiba kisebb? Ez természetesen attól függ, hogy milyen konkrét számmal közelítenek. Általában pozitív számok lekerekítésekor használja a következő szabályt:

Ezt a szabályt alkalmazzuk az ebben a szakaszban szereplő valamennyi számra; a megfontolt számokra úgy választunk ki azokat a közelítéseket, amelyeknél a hiba a legkisebb.
1) = 3,141592. Pontossága 0,001, 3,142; itt az első eldobott számjegy 5 (a negyedik helyen a tizedespont után), így közelítették a felesleget.
Akár 0,0001 3,1416, van - és itt a megközelítést a felesleges, öntött az első számjegy (az ötödik helyen a tizedesvessző után) a 9. De pontossággal 0,01 kell venni azt a megközelítést, hogy nem a: 3.14.
2) = 2,236. Pontossága 0,01, mi 2,24 (közelítés a felesleges).
3) 2 + = 4,236. Pontossága 0,01, van 2 + 4.24 (közelítés a felesleges).
4) = 0,31818. A 0,001-es pontossággal 0,318 (hiba közelítése).
Tekintsük az utolsó példát részletesebben. Vegye meg a koordinátarendszer kibővített töredékét (114. ábra).
A pont a [0.318, 0.319] szegmenshez tartozik, ezért a szegmens végeitől való távolság nem haladja meg a szegmens hosszát. A pont távolságai a szegmens végeitől egyenlőek, a [0.318, 0.319] intervallum pedig 0,001. Ezért u
Tehát mindkét esetben (és a hiba számának közelítésével, és a felesleggel való közelítésével) a hiba nem haladja meg a 0.001 értéket.
Eddig azt mondtuk: közelítés pontossággal 0,01, akár 0,001, stb Most már tudjuk, hogy a dolgok sorrendben a terminológia használata.
Ha a a x és a x számok hozzávetőleges értéke. hogy a közelítési hiba nem haladja meg a h értéket, vagy hogy az x szám megegyezik az a számmal a h-ig.
Miért fontos megtalálni a számok hozzávetőleges értékét? Az a tény, hogy gyakorlatilag lehetetlen végtelen tizedesjegyekkel működtetni, és felhasználni őket a mennyiségek mérésére. A gyakorlatban sok esetben a pontos értékek helyett a becslések előre meghatározott pontossággal (hiba) történnek. Ez az elképzelés szintén be van ágyazva a számológépekbe, amelyeken megjelenik a végső decimális törtrész, vagyis a képernyőn megjelenő szám közelítése (ritkán kivételt képez, ha a kimenet egy véges tizedes tört, amely a képernyőn illeszkedik).
A matematika letölthető leckékének gyűjteménye. naptár-tematikus tervezés, tankönyvek minden témában online
Ha bármilyen korrekció vagy javaslata van ehhez a leckéhez, írjon nekünk.
Ha látni szeretné a leckék más módosításait és kívánságait, nézze meg itt - Oktatási Fórum.