Hogyan találjuk meg a gyémánt magasságát, ha a lábak és oldalak ismeretesek

Rhombus - egy geometriai alak, amelyben az összes oldal egyenlő, így annak kerülete, mint a kerülete a tér oldalán szorozva 4. A terület rombusz függ nemcsak az oldalán, hanem a magasság, hiszen gyémánt egy paralelogramma, ezt a képletet kölcsönzött őt. Területének kiszámítására egy rombusz van szükség, hogy szaporodnak a magasságot az ő oldalán. P = 4a S = ah

A rombusz sarkai szintén a magassághoz kapcsolódnak, mivel négyszögletes háromszöget alkot a rhombusban. Az a szög szinája a gyémántban megegyezik a magasság, mint láb, a rombusz oldalához viszonyított arányával, mint a hypotenuse. A β szög 180 fokos és az α szög különbségével érhető el. (Fig.115.1) sin⁡α = h / a β = 180 ° -α

A gyémánt bármely szögének ismeretében megtalálja az átlóit. Mivel az átlós rombusz metszik egymást derékszögben, ők osztják a rombusz négy egybevágó derékszögű háromszögek szárai, amelyek félig az átlók és az átfogó - az oldalán a gyémánt. Ennek megfelelően minden ilyen háromszögben a szögek megegyeznek a rombusz szögének felével. Számítsuk ki az átlósokat az α szöggel, azáltal, hogy a rombusz oldalát a szinusz vagy a koszin α-vel szoroztuk. (Ábra.115.2) d_1 = egy sin⁡ 〖α / 2〗 d_1 = egy cos⁡ 〖α / 2〗

Mivel a rombusz egy egyenlő oldalú sokszög, így egy kör is beilleszthető. Az ívelt kör sugara összeköti középpontját a diagonálok metszéspontján és a rombusz oldalán egy merőleges metszettel. Mivel a gyémántban merőleges merőleges a magasság, a fent ismertetett tulajdonságokkal kombinálva megállapítható, hogy a sugár fele a gyémánt magassága. (151. ábra) r = h / 2

Van egy ilyen képlet a tetszőleges négyszögnek a dl, d2 átlóval, amelynek szöge között φ: S = ½d₁d2 sin φ. Abban az esetben, egy rombusz (a szög közötti átlós vonal), ez adja az S = ½ d₁d₂ = ½ · 14 · 48 = 336. Másrészt, S = ah, ahol egy - oldalán, h - magassága rombusz. Oldalsó megtalálható a Pitagorasz-tétel, tekinthető egy negyed-háromszög rombusz: a² = (14/2) ² + (48/2) ² = 49 + 576 = 625 = 25², a = 25. Következésképpen, 336 = S = 25h, ahol h = 13,44 (cm). Az általános formája: S = ½ d₁d₂ = ah = ½√ (d₁² + d₂²) · H, H = d₁d₂ / √ (d₁² + d₂²). A trapéz minden rosszabb. Csak az átlón keresztül (anélkül, hogy tudnánk más elemeket) a területet nem lehet kifejezni. ========== FÜGGELÉK Az ABCD legyen trapéz (BC

vegye figyelembe a rombusz négyszögletes háromszögét, és két lába egyenlő az átlósok félévei. Igen láb 7 és 24. Ezután oldalán a rombusz 25 m magassága Pythagorasz cukorka 7 * 24/25 - van a derékszögű háromszög: két láb szaporodnak és osztódnak a átfogója úgy, hogy a magassága 6,72 ------- ------

a trapéz területe, ismerve a diagonyt 1/2 d1 * d2 * sin (a)? de a az átló közötti szög. HA EZEK A BILLENTYŰZET EGYENLŐDIK ÉS DIAGONÁLT EGYENLŐT

Tudva, hogy az átlós, megtalálja a rombusz magasságát. A pitagorai tétel segíteni fog ebben. És bár a jobb szögű háromszögeket érinti, ezek a gyémántban is léteznek - két átlós d1 és d2 metszéspontja alkotja őket:

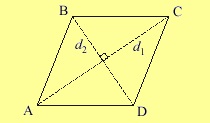
Képzeld el, hogy az 1-es átló 30 centiméter, az átló pedig 2-40 cm.

A magasság kiszámításához meg kell számolnunk a gyémánt területét és az egyik lábszár méretét (a gyémántban, mint tudjátok, ugyanazok).

Tehát a mi cselekedeteink:

1. Az oldal nagyságát a pitagorai tétel alapján számítjuk ki. A BC oldala a BXD háromszög hipoténusa (mivel az a tompás szöggel szemben helyezkedik el) (X a d1 és d2 átlós metszéspontja). Tehát a téren lévő oldal mérete megegyezik a BX és az XC oldalak négyzetének összegével. Méreteik is ismertek (a rombusz metszésének átlói félig osztva) - ez 20 és 15 centiméter. Kiderül, hogy a BC oldal hossza egyenlő a 20 négyzet és a 15 négyzet gyökereivel. Az átló négyzetének összege 625, és ha ezt a számot kivesszük a gyökérből, akkor a lábméret 25 centiméterrel egyenlő.
2. Számítsa ki a gyémánt területét két átló segítségével. Ehhez szorozzuk meg a d1-et d2-vel, és osztjuk az eredményt 2-vel. Kiderül: 30 szorozva 40 (= 1200) és osztva 2-elhagyással 600 cm-es négyzet. - ez a gyémánt területe.
3. Most számold ki a magasságot, ismerd meg az oldal hosszát és a gyémánt területét. Ehhez meg kell osztanod a területet a láb hossza szerint (ez a képlet a gyémánt magasságának kiszámításához): 1200 osztja el a 25-öt - 48 cm-t hagy. Ez a végső válasz.

Hogyan találjuk meg a gyémánt magasságát, ha ismerjük a területet és a kerületet (mely képlet)?

Ismerje meg az összes formulát a gyémánt terület kiszámításához:

A magasság megismeréséhez szükségünk van az első képletre (terület = magasság szorozva az oldal hosszával).

Tegyük fel, hogy a perem 124 cm, a terület pedig 155 cm.

Arra a kézbe kerülünk, hogy a rombusznak minden oldala megegyezik, mivel a peremrésze négyszer annyi, mint az egyik lábának hossza.

A gyémánt magasságának kiszámításához ismernie kell a láb méretét. Íme néhány olyan tevékenység, amely segít a probléma megoldásában:

1. Találjuk meg a rhomb oldalának hosszát egy ismert kerületen keresztül. Ehhez a peremfrekvencia értékét (124) 4-tel osztják meg, és 31 centiméter értéket kapunk - a láb hossza.
2. A magasságot a térfogati képlet segítségével számítjuk ki. Ossza el a területet (155 cm-es négyzet) a lábszár méretétől (31 cm) és 5 cm-t kapjon - ez a geometriai alakzat magassága.

Hogyan találjuk meg a gyémánt magasságát, ha az oldal és a szög ismeretes?

A feladat bonyolultnak tűnik, de nem az. Képzeljük el, hogy a rombusz lábának mérete megegyezik a három gyökerével és a szög 90 fokkal.

A magasság dimenziójának kiszámításához használja a gyémánt négyzet képletet (az oldalsó szorzás a szög szinuszával). Hogy megtudd a szinusz minden fokát, használja a válaszomban. A 90 fokos szinusz 1-es, tehát nagyon könnyű megtalálni a magasságot. Kiderül, hogy a terület egyenlő az oldal (3) hosszának négyzetével, megszorozva a 90 gr szinusz. (1), amely a végén egy válasz-3 cm-es négyzet.

Ezután oszd meg a kapott területet a láb méretével: 3 osztva a 3 gyökerével, és kapjuk meg a rombusz magasságát -√3.

Hogyan lehet kiszámítani a gyémánt magasságát, ha az oldal és az átló ismeretes?

Ebben a problémában egy derékszögű háromszöget kell használni, amelyet az átlós metszés alkot.

Tegyük fel, hogy az oldal 10 cm, az átló pedig 12 cm.

1. Megtaláljuk a második átló felének méretét a pitagorai tétel segítségével. A hipotenuzus ebben az esetben az oldala, ezért az átló fele megegyezik a láb négyzetének (10 a négyzetben) és az ismert átlós (6 négyzet) fele négyzetének különbségével. Kiderül, hogy 100-ról 36-ra kell vinni - 64 centiméterünk van. Szedjük ki a gyökeret ebből a számból, és szerezzük be a második átlós felét - 8 cm-t, és a teljes hosszúság 16 centiméter.
2. Számítsd ki a gyémánt területét két átló segítségével. Szorozzuk meg az első átló hosszát (12 cm) a második (16 cm) hosszúsággal és osztjuk meg 2 - 96 cm-es négyzetet kapunk. (ez a gyémánt területe).
3. Számítjuk ki a magasságot, ismerjük az oldal és a terület méretét. Ehhez 96 osztja 10 - 9,6 cm-t hagy - ez a végső válasz.

Azt javaslom, olvasd el még mindig