Fejezet Hamilton ciklusokat
2. fejezet Hamilton kör
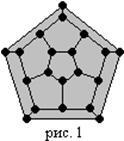
§1. Alapfogalmak és meghatározások
Ha a gráf egy egyszerű ciklus, amely minden a gráf csak egyszer, egy ilyen ciklust nevezzük Hamilton kör, és a grafikon az úgynevezett Hamilton grafikonon. Graph, amely tartalmaz egy egyszerű utat minden csúcsba, szemi-Hamilton. Ez a meghatározás lehet terjeszteni irányított gráf, ha az áramlási pálya tekintették orientált.
A Hamilton-kör nem feltétlenül tartalmazza az összes szélei a grafikonon. Egyértelmű, hogy a Hamilton csak egy gráf, és minden Hamilton gráf félig Hamilton. Megjegyezzük, hogy a Hamilton-kör létezik nem minden oszlopra.
Bármely G gráf lehet alakítani egy Hamilton gráf hozzáadásával elegendő számú csúcsok. Ehhez, például ahhoz, hogy felsők v1, ..., vp G hozzá egy vertex u1, ..., fel, és több bordát.
A foka v pont az élek száma d (v), az eset, hogy ez, ahol a hurok kétszer számít. Abban az esetben, egy irányított gráf megkülönböztetni fokú do (v) a kimenő ívek és di (V) - a bejövő.
2. §. Feltételei fennállásának Hamilton kör
Ellentétben Euler gráf, ahol van egy kritérium egy gráf Euler, Hamilton grafikonokat ez a kritérium nem. Sőt, a feladata, hogy megvizsgálja, hogy létezik egy Hamilton-kör probléma NP-teljes. A legtöbb ismert tények a következők: „ha a G gráf elegendő számú élek, a gráf Hamilton.” Íme néhány ilyen tételek.
Dirac-tétel. Ha a gráf G (V, E) c n csúcsú (n ≥ 3) megfelel annak a feltételnek d (v) ≥ n / 2 bármely v V, akkor a G gráf Hamilton.
Éppen ellenkezőleg. Legyen G - Nem Hamilton. G hozzá a minimális számú új csúcsok u1, ..., un, amely egyesíti őket az összes csúcsot G úgy, hogy G „: = G + u1 + ... + un volt Hamilton.
Legyen v, u1, w, ..., v - Hamilton kör egy gráf G 'és v G, u1 G', u1 G. ilyen pontpár v és u1 a Hamilton-kör létezik, mert különben a G gráf lenne Hamilton. Ezután, W G, W, különben a vertex u1 nem volt szükség. Továbbá, a nem-szomszédos v csúcs a vertex w, különben a vertex u1 nem volt szükség.
Továbbá, ha egy ciklus v, u1, w, ..., u 'w', ..., v pedig egy csúcs w 'szomszédos csúcs w, akkor a v csúcs' nem szomszédos a v csúcs, mert különben tudtunk építeni egy Hamilton-kör v, v '..., W, W', ..., V nélkül felsők u1, vesz egy szekvenciát a csúcsok w, ..., v „fordított sorrendben. Ebből következik, hogy a csúcsok száma a gráf G”, nem szomszédos az v, nem kevesebb, mint a csúcsok száma szomszédos w. Azonban, bármilyen vertex W G gráf d (w) ≥ p / 2 + n az építési, ideértve a d (v) ≥ p / 2 + n. A teljes csúcsok száma (szomszédos és nem-szomszédos v) n + p-1. Így van:
n + p-1 = d (v) + d (V) ≥ d (w) + d (v) ≥ p / 2 + n + p / 2 + n = 2n + p.
Következésképpen, 0 ≥ n + 1, amely ellentmond annak a feltételezésnek, hogy n> 0.
Ore tétel. Ha a csúcsok száma a G gráf (V, E) n ≥ 3 és bármely két nem szomszédos csúcsok u és v kielégíti az egyenlőtlenséget:
d (u) + d (v) ≥ n és (u, v) E, akkor a G gráf - Hamilton.
Egy gráf egy Hamilton-ciklust, ha az alábbi feltételek mellett:
Pausch feltételek: d (vk) ≥ k + 1 k Bondy feltételek: a d (VI) ≤ i és d (vk) ≤ k => d (vi) + d (vk) ≥n (k ≠ i) Feltételek hiányzik: a d (vk) ≤ k ≤ n / 2 => d (VN-k) ≥ n-k. Továbbá az is ismert, hogy szinte az összes Hamilton grafikonok, hogy van, ahol H (p) - a készlet Hamilton grafikonokat p csúcsok, és G (p) - a készlet minden grafikonokat p csúcsok. Így a probléma megtalálásának Hamilton kör, vagy azzal egyenértékű az utazó ügynök probléma gyakorlatilag kereslet, de nem ismert (és valószínűleg nem is létezik) hatékony algoritmust megoldására. Egy példa a grafikon, ha nem ez a feltétele Dirac-tétel, de a grafikon Hamilton. N = 8; d (VI) = 3; 3 ≥ 8/2 = 4 nem egy Hamilton-gráf, de van egy Hamilton kör: M = (1, 2, 3, 4, 5, 6, 7, 8, 1) 3. §. Kapcsolatos feladatokat a keresést Hamilton ciklusokat Egyes iparágakban a következő ütemezési probléma merül fel. N Ez előállításához szükséges termékek használatával egyetlen típusú berendezések. A készüléket be kell állítani miután a terméket állítottak elő pi (de még mielőtt a gyártás a termék elkezd pj), attól függően, hogy a kombináció a (pi, pj). Az ára átkonfigurálva berendezés állandó, és független a gyártott termékek. Tegyük fel, hogy ezeket a termékeket gyártják Végtelenítve, hogy miután az utolsó termelés az n termékek újra folytatják ugyanazt a fix ciklusban termelés az első termék. Felmerül a kérdés, ciklikus sorrend termelési pi (i = 1,2, ..., n), amely nem igényel újrakonfigurálását berendezések is ott található. Ha elképzeljük ezt a feladatot formájában egy irányított gráf, a válasz erre a kérdésre attól függ, hogy az irányított gráf egy Hamilton-kör, vagy sem. Ha van egy ciklikus sorozata termékek, amely nem igényel átalakítását berendezés, mit kell egy gyártási sorrend a legalacsonyabb költség vándorolni, azaz a igényli a legkevesebb szükséges perenastroek? Így tartjuk a következő két probléma. Probléma 1. Dan G irányított gráf, szükséges, hogy megtalálják a Hamilton kör G-ben (vagy az összes ciklus), ha van legalább egy ilyen ciklus. Probléma 2. Dan orientált teljes ciklus G, amely ívek vannak rendelve tetszőleges tömeg C = [CIJ], hogy megtalálják a Hamilton kör, amelynek a legkisebb a teljes súlyt. Meg kell jegyezni, hogy ha egy irányított gráf G nem teljes, akkor lehet tekinteni, mint egy teljes irányított gráf, tulajdonítja a hiányzó ívek végtelen tömeg.
Kapcsolódó cikkek