Lineáris függetlenség - előadások matematike- 6. rész - Műveletek mátrixok 3-selejtező

lineáris függetlenség

El lineáris kombinációja sorokban. e2. ek az úgynevezett szorzatösszegében e sorok tetszőleges valós számok:
e = l El + 2 e2 +. + k ek. ahol l. 2. k - tetszőleges számú (lineáris kombinációjával együtthatók).






El-line mátrixban. e2. em az úgynevezett lineárisan függ. Ha vannak számok l. 2. m. nem minden nulla, a lineáris kombinációja a sorok a mátrix egyenlő a nulla vonal:
l El + 2 e2 +. + m em = 0, ahol a 0 = (0 0. 0).

A lineáris függését a sorok a mátrix azt jelenti, hogy legalább egy sor a mátrix egy lineáris kombinációja a többiek. Valóban, tegyük fel meghatározottság utolsó m faktor  0. Ezután elosztjuk mindkét oldalról m. megkapjuk azt a kifejezést utolsó sort. lineáris kombinációjával a fennmaradó sorok:
em = (l / m) El + (2 / m) e2 +. + (m-1 / m) em-1.
Ha egy lineáris kombinációja a sorok egyenlő nullával akkor és csak akkor, ha minden együttható nulla, azaz l El + 2 e2 +. + m em = 0  k = 0 k, a sor az úgynevezett lineárisan független.
A tétel a rangot a mátrixban. A rangsorban a mátrix megegyezik a maximális számát lineárisan független sorok vagy oszlopok. amelyen keresztül lehet lineárisan kifejezni minden őt más sorok vagy oszlopok.
Belátjuk ez a tétel. Hagyja, hogy a mátrix m x n mérete rangot r (R (A)  perc). Következésképpen, van egy nem nulla kisebb r-ed rendű. Az ilyen kisebb lesz az úgynevezett alap. Mert határozottságot, legyen ez a minor

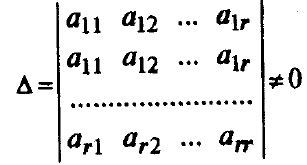
Sorok Ezt a kisebb is lehet nevezni az alap.
Lássuk be, hogy el sorban a mátrixban. e2. er lineárisan független. Tegyük fel, hogy éppen ellenkezőleg, azaz az egyik ilyen vonalak, például az R-i jelentése egy lineáris kombinációja a többiek: ER = l El + 2 e2 +. + r-1 ER-1 = 0. Ekkor, ha elemek kivonni r-edik sor elemeit az 1. sor szorozva l. elemei a 2. sor szorozva 2. stb Végül, az elemek (r-1) -edik sorban, szorozva r-1. az r-edik sorban lesz nulla. Ebben az esetben a tulajdonságait meghatározó a meghatározója a fenti nem kell megváltoztatni. és így nullának kell lennie. Ez ellentmondás, lineáris függetlenség a sorok bizonyult.
Most bebizonyítjuk, hogy bármely (r + 1) a mátrix sorai lineárisan függ, azaz a bármilyen karaktersorozat lehet kifejezni alapján.

Kiegészítés korábban tekinthető kisebb egy másik vonal (i-edik) és a másik oszlop (j-m). Az eredmény kisebb (r + 1) -edik sorrendben, ami a definíció szerint nulla helyezés:

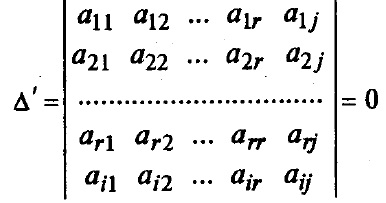
Nagyítás által elemei a j-edik oszlop. Itt nemrég kofaktor Aij egybeesik az alap kisebb   0  Aij  0. Ezért tudjuk osztani mindkét oldalán az egyenlet által Aij. Ez lehetővé teszi, hogy kifejezze eleme :.

Ha rögzítjük a sor számát (i), azt találjuk, hogy minden j elemek az i-edik sorban lineáris kombinációi elemeinek alapvető vonalak: vagyis minden sorban a mátrix egy lineáris kombinációja alapján.