Funkciók és grafikonok
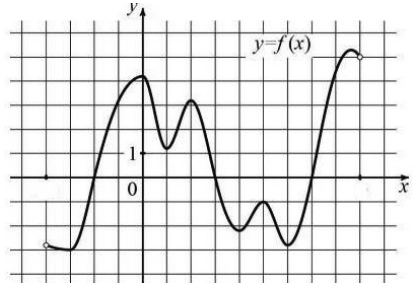
Ábra. 1. A grafikon a $ y = f (x) $.
Rendszere rajzoló funkciókat
- A domén definíció $ D (f) $ és tartományban $ E (f) $.
- Paritás ($ f \ left (x \ right) = f \ left (-x \ right)) $, páratlan ($ f \ left (x \ right) = - f \ left (x \ right)) $, a periodicitás ( $ f \ left (x \ right) = f \ left (x + T \ right)) $.
- A metszéspontok a koordinátarendszer intervallumokban, ahol $ f \ left (x \ right)> 0 $ és $ f \ left (x \ right)
- Teszt növekedése $ '\ left (x \ right)> 0) $, a csökkenés $' \ left (x \ right)
- Vizsgáljuk az inflexiós pontot, és időközönként konvexitás $ (f ^ \ left (x \ right)> 0) $ konkáv ($ f ^ \ left (x \ right)
- Számoljuk ki a korlátokat a határokat a domaint.
- Értékek további pontokat.
- Ütemezése.
szabályok ábrázolási
- $ Y = f (x-a) $ nyert grafikon $ f (x) $ váltani tengelyirányban $ Ox $ $ | a | $ jogot, ha $ a> 0 $ és balra, ha $ a
- $ Y = f \ left (x \ right) + b $ nyert grafikon $ f (x) $ eltolódás tengelyirányban $ Oy $, hogy $ | b | $ felfelé, ha $ b> 0 $ és le, ha $ \ b
- $ Y = f (kx) $ nyert grafikon $ f (x) $ $ kompressziós tengely Oy $, ha $ k> 1 $ és nyúlás, ha $ 0
- $ Y = kf (x) $ nyerik a grafikonon a $ f (x) $ húzódó tengelye $ Ox $ a $ k $ alkalommal, ha $ k> 1 $, és tömörítés, hogy a tengely $ Ox $ a $ \ frac $ újra, ha $ 0
- $ Y = f (-x) $ nyert grafikon $ f (x) $ szimmetrikus reflexió a tengely körül $ Oy $.
- $ Y = -f (x) $ nyert grafikon $ f (x) $ szimmetrikus reflexió a tengely körül $ Ox $.
- $ Y = | f \ left (x \ right) | $ nyerik a grafikonon a $ f (x) $ a következőképpen: a grafikon részei $ f (x) $, fölött fekvő tengelye $ Ox $ változatlan marad, és a fekvő alatt $ Ox $ megjelenik szimmetrikusan a tengelyre Oy $ $.
- $ Y = f \ bal (| x | \ right) $ nyerik a grafikonon a $ f (x) $ a következőképpen: a grafikon részei $ f (x) $, amely abban rejlik, hogy a megfelelő tengely $ Oy $ változatlan marad, akkor ez a rész jelenik szimmetrikusan a tengelyre Oy $ $ helyett a részét, amely abban rejlik, hogy a bal oldalon $ Oy $.
Egy példa a kutatás és az építőipar a funkció
Hogy vizsgálja meg a funkció és a kivitelezést a grafikon:
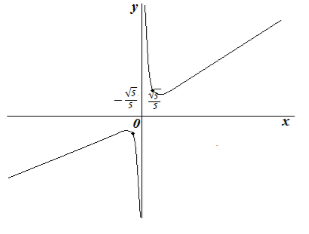
\ [Y = \ frac \]
- A domain a meghatározás: $ \ left (- \ infty, 0 \ right) (0, \ infty) $. Érték tartomány: $ \ left (- \ infty, 1-2 \ sqrt \ right] [1 + 2 \ sqrt \ infty) $
- funkciót, vagy akár, vagy páratlan, nem periodikus.
- metszéspontja a koordináta-tengely nem.
Ha a $ x \ in \ left (- \ infty, 0 \ right) $ függvény negatív, a $ x \ in \ left (0, \ infty \ right) $ pozitív.
időközönként módszer azt találjuk, hogy
A függvény növekszik $ x \ in \ left (- \ infty, - \ frac> \ right) \ left (\ frac> \ infty \ right) $ és csökken, ha $ x \ in \ left (- \ frac> 0 \ right) \ left (0, \ frac> \ right) $
Maximális funkció: $ \ left (- \ frac> 1-2 \ sqrt \ right) $
Minimális funkció: $ \ left (\ frac>, 1 + 2 \ sqrt \ right) $
intervallum módszer, amely a függvény konvex az $ x \ in \ left (0, \ infty \ right) $ és konkáv $ x \ in \ left (- \ infty, 0 \ right) $