Lineáris operátorok és funkcionálok normált terekben
másolat
1 Laboratóriumi munka 9 lineáris operátor és funkcionális egy normált térben. Norm lineáris operátor és funkcionális. C O O V N N E P A N I T I I I T E R O E M N Meghatározás. Legyen vektor terek fölött ugyanazon a területen (= R vagy C). A következő. domain D () és domain R () értékeket a lineáris üzemben hívják, ha van ilyen, y és. ) (Y) y (additivitás); ) () (Homogenitás). Jelölje (,) a több lineáris operátorok a tartomány meghatározásának, amely egybeesik E. A, (,), és meghatározza operátorok (,) képletek. def def (); (). Ekkor (,) lesz vektortér. Abban az esetben, ha (a mező vektortér!), Az elemek (,) egy lineáris működőképes. Tegyük fel most, hogy meghatározott szabályok i (i,), azaz normalizált tér (Norm). Definíció. Operátor () függvény korlátos B-ből, ha létezik egy olyan c konstans, melyre minden van az egyenlő c. Definíció. Norm operátor (,) az a szám, def sup. Meg lehet mutatni, hogy a definíció c. a legnagyobb alsó határa a beállított állandók
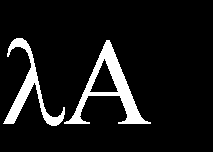
2 Tétel. Legyen (,) ahol, Norm. Ekkor a következő állítások ekvivalensek. ) Az üzemben a folyamatos üzemben; ) Operator korlátos üzemeltetőt, hogy; ). Legyen (,) ahol, Norm. Az alábbi relációk :); ); ). Ha tehát korlátos operátorok, a szolgáltatók is korlátozott. Következésképpen, ha L jelöli (,) a készlet minden korlátos lineáris operátorok, akkor L (,) vektor altér (,). Ez tétel. Ha Norm, és Banach (Ba), akkor L (,) Ba. Az összes fenti feltétel vonatkozik a funkcionális. Ebben az esetben, az arány, így a funkcionális F (,) nevezzük határolva Norm, ha létezik olyan C konstans, melyre f () ° C-on az összes. Ezután a norma f száma def f sup f (), ha c. f () c. Mivel Ba, a tétel L (,) Ba. Definíció. Banach tér L (,), amely lineáris funkcionálok korlátozódik, amelyek jelölése * és az úgynevezett duális tér E. Irodalom: [] pp 9-56 ;. [] P 8-5 .; [5] p H A D A ÉS B
3. Tegyük fel, hogy Norm. Domain keresése def D (). üzemeltető és annak megállapítása, hogy ez egybeesik. Ha D () Norm, hogy megtudja, hogy a gazdasági szereplő egy korlátos lineáris operátor D () in? E. L c. c l. L [,] L [,] () (t) t (s). L [,] L [,] () (t) (t) .5 L [,] L [,] () (t) (t) .6 C [,] C [,] () (t) ( t) .7 C [,] C () [,] () (t) (t) .8 C () [,] C [,] () (t) (t) .9 c R. l l. l l. L [-,] L [-,] () (t) (5, t). C [,] R () (t) () (). L [-,] L [-,] () (t) t (s) .5 L `[,] L [,] () (t) (t) zadachi.5 oldatot. Találunk D () L [,]. L [,] a domain az üzemeltető. Mivel 8 (t) (t), majd a D (A) = L L
if ($ this-> show_pages_images $ PAGE_NUM doc [ 'images_node_id']) 
4 (y) y. Ezért, az üzemeltető nem lineáris D (), és ennek következtében is korlátozott. -5. Meghatározza, hogy a képlet egy korlátos lineáris operátor. Abban az esetben, korlátos operátorok találják normális. A szorzás művelet. C [,] C [,] () (t) (t t) (t). C [-,] C [,] () (t) (t t) (t). L [,] L [,] () (t) t (t). L [,] L [,] () (t) (tt) (t) .5 L [-,] L [-,] () (t) t (t) .6 L [-,] L [, ] () (t) t (t) .7 L [,] L [,] () (t) (t) (t) .8 C [-,] C [,] () (t) (tt) (t) 0,9 L [-,] L [-,] () (t) t (t). C () [-,] C [,] () (t) si t (t). L [,] L [,] () (t) t (t). C [-,] C [-,] () (t) (t) (t), t [, [(t t) (t), t [,]. C [,] L [,] () (t) t (t) t (t), t [,]. L [-,] L [-,] () (t), t [, [Solution. Field az üzemeltető D () L [-,] (terméke (t) egy folytonos függvény nem "kimenet" a termék az L [-,]). Lineáris operátorok nyilvánvaló. Mivel az L [-,]
5 L t t t [,] () () L
6. L [,] L [,] () (t) t (t). L [-,] L [,] () (t) t (t) megoldás. Legyen L [-,]. Akkor T (t) L [,] u t du t t u = du (u) (u) (u) (u) du u (u) du L [,]. Ebből összefüggésben az következik, hogy a D () L [-,]. Nyilvánvaló, hogy az üzemeltető lineáris származó bevált egyenlőtlenség A korlátos és. Tekintsük a szekvenciája funkciók (t) (t) L [,]. Majd a [,] L [,] sup L [,] sup sup (u) du L [,] L [,] sup sup 5 Így 5 5 5 Figyelembe véve az előző, már. Az üzemeltetők sorrendben terek l l (.) 5
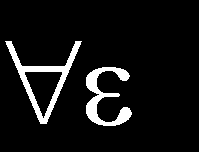
7. l l (.). c c (.). l l. 5 l l. 6 l l. 7 l l. 8 c c. 9 c si C. si. l l (.). L c. l l. l c (.). l l. ahol M, N oldat. Mivel a L sup sup, a D () l, és a linearitást az operátor könnyen ellenőrizhető. Ennélfogva, is sup I. Meghatározásával legalább a felső korlát létezik olyan, hogy az I., akkor L (.) L, L és sup l I. eljárva az utolsó egyenlőtlenség limit I sup, azaz sup 5. Az integrál operátor kap 6
8 5. L [,] L [,] () (t) ts (ek) 5. L [,] L [,] () (t) (t) s (s) 5. C [,] L [ ,] () (t) (ts) (s) 5. L [,] C [-,] () (t) ts (s) 5,5 L [,] LT (t). t (t), L [,] l t (t). t (t), L [,] L [-,] () (t) ts (ek) 5,8 C [-,] L [,] () (t) TSIG s (s), 5,9 L [,] L [ ,] () (t) ts (ek) 5. L [,] L [,] () (t) (t) s (s) 5. C [,] L [,] () (t) sig ( s) (s) t () 5. L [-,] L [,] () (t) (t) s (s) 5. C [,] C [,] () (t) (ts) ( s) 5. L [,] LT (t). t (t). 7
9. megoldási lehetőség 5. Legyen L [,]. Akkor L t (t) (t) L. [,] Ezért, D () L [,] és a linearitást az üzemeltető legyen szerves linearitást. A létrehozott egyenlőtlenség tamkzhe, hogy 8. Másrészről, ha (t) (t), majd, és az L, [,] sup L [,] l sup l sup t sup () 8. Következésképpen, hagyja Ba, K vagy C. Meghatározza, hogy a korlátos lineáris funkcionális képletű f. Ha igen, találnak normális. f 6. c c f () lim 6. L R f () 8
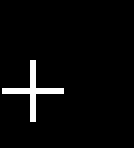
10 6. L R 6. c C 6,5 l R 6.6 c R f () f () (i) f () f () 6,7 l C F () 6.8 c R f () L R f () 6. L R f () 6. C l f () l C I 6. f () 6. R c f () L C lim 6. f () Megoldás 6. Linearitás funkcionális könnyen ellenőrizhető. Legyen l. Ezután a Cauchy-Schwarz-egyenlőtlenség, van. l f () () Ennélfogva, a D (f) l, f határolja funkcionális l, és, hogy az állandó f c. Megmutatjuk, hogy ez a legkisebb az összes lehetséges (). Elegendő, hogy jelezze az ilyen nem nulla elemet l, amelyre () válik egy lánc egyenlőségek. A egyenlőség () zavarhatja alkalmazása után Cauchy-Schwarz-egyenlőtlenség. Az utóbbi nem sérti az egyenlőség esetén * 9
11. N. f () * * Egy idő a * (.), 8. Tehát f. 7. L [,] R f () t (t) 7. L [,] C f () ez (t) 7. C [,] R f () () () 7. C [,] R f () lim (t) 7,5 L [,] C f () t (t) 7,6 L [-,] R f () t (t) 7,7 L [,] R f () t (t) 7,8 L 6 [ ,] R f () t (t) 7,9 C () [,] C f () () i () 7. C () [,] R f () (t) (t) 7. C () [ -,] C f () () 7. C () [,] C f () i () () 7. L [,] R f () t (t) 7. L [,] C f () ez (t) f * és
12 Solution 7. lineáris funkcionális ered az integrál linearitást. Legyen L [,]. Aztán, hogy a változás a változók az integrál, majd alkalmazása a Cauchy-Schwarz-egyenlőtlenség, megkapjuk az f () t (t) u t u t udu u u u du du u du () (). () Ezért a D (f) l, a funkcionalitás korlátozott, és f. Vegye * (u) u (miért?), Akkor (), van * * f () u u u du du. Ebből következik, hogy az állandó c lehetséges. Ezért f () a legrövidebb az összes Változatok Variant Variant Variant munkát Variant Variant Variant Variant Variant Variant Variant Variant Variant Variant Variant Variant Variant
13 Variant Variant Variant Variant Variant Variant Variant Variant Variant Variant D D O T L N I E A L H N E W A D A B u és v P R A F E S H J. Igazoljuk, hogy a funkcionális f. (T) (T) R (t) C () [,] folyamatos. 5. Igazoljuk, hogy a funkcionális f. (T) (T) R jelentése lineáris és lineáris határtalan altér C () [,] normált teret C [,]. 6. L úgy a kezelő (.) (.). Semmilyen arra korlátozódik, hogy az l? Találd meg normális. 7. Tegyük fel, hogy az üzemeltető a szorzataként korlátozott mérhető függvény a (), eljárva a térben L p (,). Bizonyítsuk be, hogy korlátozott, és találja meg a normális. 8. Keresse meg a norma a személyazonosság járva LP [a, b] LQ [a, b] p q.
Laboratóriumi munka spektrumát az üzemeltető. C O O V N N E P A N I T I I I T E R O E M N Let. korlátos lineáris operátor egy Banach-tér felett a területen. C. meghatározása. C pont egy reguláris
1 függvények folytonosak az intervallum (Bolzano Cauchy-tétel, Weierstrass Cantor). Funkcionális folytonos a kompakt. 1.1 A Bolzano-tétel 1. tétel (Bolzano-Cauchy) Legyen az f függvény folytonos az [a, b], ahol F (a), F (b). Ezután, tetszőleges számú C, közötti F (a) és f (b) van egy olyan pont γ (a, b), hogy f (γ) = C igazolása. Tegyük fel például, f (a) = A 0. Elég azt mutatják, hogy létezik egy pont γ (a, b), hogy g (γ) = 0. elosztjuk az intervallum [a, b] X pont 0 két egyenlő a hossza a szegmens, akkor vagy a g (x 0) = 0, és így a kívánt ponton γ = x 0 található, vagy g (x 0) 0, majd végeinél az egyik keletkező hézagokat g veszi értékeit a különböző jelek, pontosabban, a a bal végén az érték kisebb, mint nulla, a jobb - több. Jelöljük a intervallum [1, b 1], és felosztják ismét két egyenlő hosszúságú szegmens stb Ennek eredményeként, vagy egy véges számú lépésben, hogy megkapjuk a kívánt ponton γ, ahol g (γ) = 0, vagy elérjék a szekvenciáját beágyazott szegmens [n, b n] hosszúságú nullához, oly módon, hogy g (a n)