I 11 A melléklet-származék
Előadás 11 „Applications a származék a vizsgálat funkció”
Egy változtatható úgynevezett monoton, ha ez annak köszönhető, hogy változások csak egy irányban, azaz, vagy csak vozras olvadáspontú, vagy csak csökken. Nyilvánvaló, hogy a mozgás egy pont x a pozitív irányát az x-tengely monoton nő, és az ellenkező irányba - monoton csökkenő.
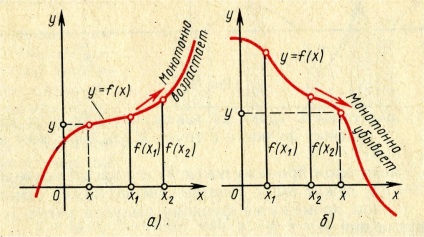
Ábra. 3. Táblázatok monoton növekvő és monoton csökkenő függvény.
Természetesen, az intervallum (a, b) Tegyük fel,-Gaeta vett a domain a funkció.
Elegendő feltétele növekvő (csökkenő) függvény. Ha a függvény az y = f (x) intervallumban differenciálható
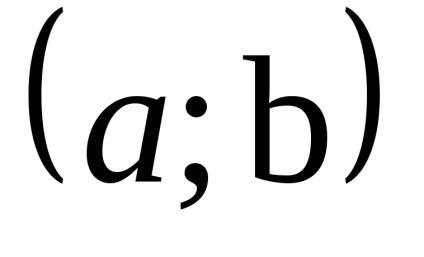
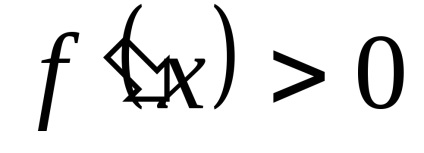
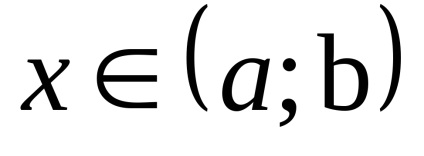
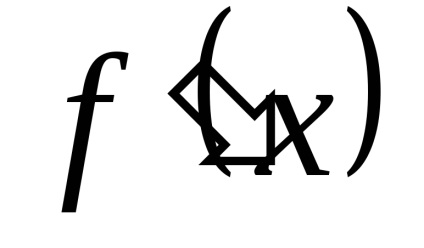
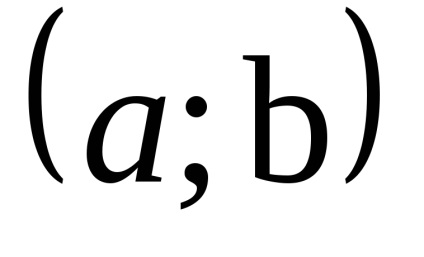
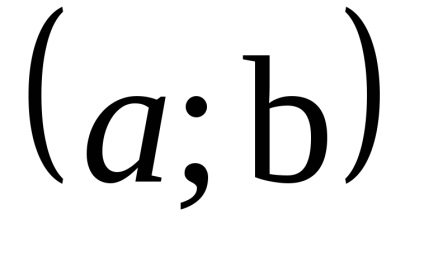
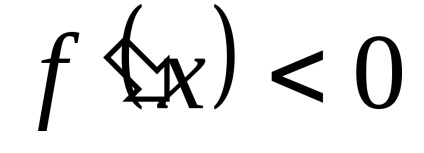
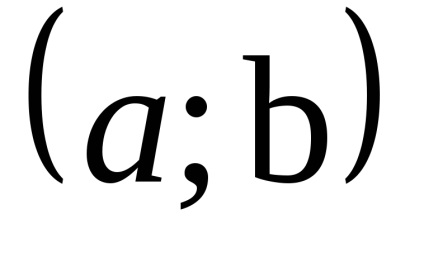
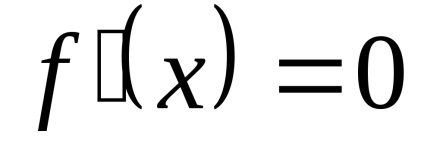
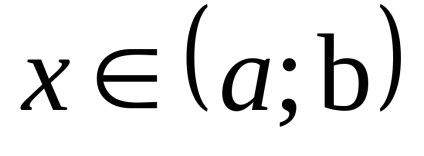
Azt mondják, hogy a függvény az y = f (x) egy lokális minimum a ponton h0є [a; b]. ha létezik olyan szomszédságában x0, teljes egészében tartalmaz, [a; b] olyan, hogy minden x. Tulajdonában van az első ezen a környéken, az egyenlőtlenséget az f (x)> f (x0).
Elegendő feltétele extrém funkciókat. A kritikus pont (pont belső tartomány a függvény, ahol a származék ezen funkció nulla vagy nem létezik) egy szélsőérték funkciót. ha a közelben ezen a ponton a derivatív változások jele, és a maximális pontot. amennyiben a származékos előjelet ettől a „+” „-”, és a minimális pontot. amennyiben a származékos előjelet az „-” és „+”.
A legnagyobb (legkisebb) értékét a folytonos függvény az y = f (x) [a; b] elérhető akár az egyik kritikus pontok, vagy az egyik a határpontok a szegmens.
Azt mondják, hogy a függvény az y = f (x) konvex felfelé x0. ha létezik olyan pont szomszédságában x0 olyan, hogy az összes pont x érintő a függvény grafikonját a ponton M0 (x0. y0) felett fekszik a grafikon (4a.). Azt mondják, hogy a függvény az y = f (x) konvex x0. ha létezik olyan pont szomszédságában x0 olyan, hogy az összes pont x érintő a függvény grafikonját egy pont M0 (x0, y0) alatt fekszik a grafikon (4b ábra.).
Ha egy bizonyos intervallumban (a; b) érintőleges minden gra-FIKU függvény y = f (x) fölött fekszenek (vagy alatt) a grafikon, majd egy adott intervallum felfelé konvex (vagy lefelé irányuló konvex).
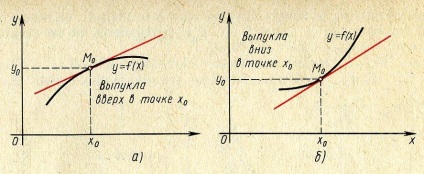
Ábra. 4. Grafikon konvex
Annak meghatározása, hogy időközönként konvexitás és inflexiós pont
A elégséges feltétele domborulata a funkció az intervallumon. Ha a második derivált f „(x) létezik intervallumban (a, b) és változások aláírására ebben az intervallumban, majd a:
1) f „(x)> 0 (+ jel), az f (x) konvex lefelé egy inter-tengely (a; b);
2) amikor az f „(x) <0 (знак - ) функция f(х) выпукла вверх на интервале (а;b).
Így, megtalálása intervallumok konkáv és konvexitási le funkció, hogy megtalálja a második pro-vizes és megoldani a egyenlőtlenség f „(x) <0 и f"(х)> 0.
M0 (x0, f (x0)) a grafikon y = f (x) a-nevezzük egy inflexiós pont ez a grafikon, ha létezik-kai szomszédságában x0, amelyen belül a függvény grafikonját y = f (x), hogy a bal és jobb oldalán a t. M0 különböző irányokba you-konvexitás.
Ábra. Az 5. ábra egy függvény, amelynek inflexiós pontnál M0 (x0, f (x0)).
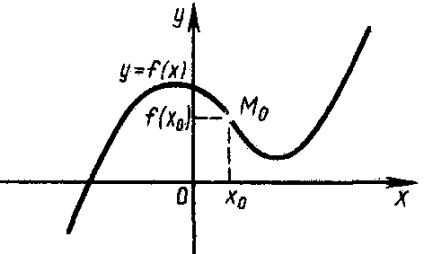
Ábra. 5. Menetrend függvényében, amelynek inflexiós
A szükséges feltétel megléte az inflexiós pont. Ha a funkció a ponton x0 van egy kanyarban, majd a második derivált ezen a ponton vagy nem létezik, vagy nulla.
A pontok, ahol a második derivált nulla, vagy nem létezik, az úgynevezett kritikus pontjait II-nd fajta. Ezeken inflexiós pontok vagy nem lehet. Ez az ügy újra a gyűrődéseket a következő tag.
Elegendő kritériuma az, hogy létezik egy inflexiós pont. Tegyük fel, hogy a funkció határozza meg, és folyamatos a szomszédságában x0. beleértve a nagyon pontot. Tegyük fel továbbá, hogy a második derivált Nye ezen a ponton egyenlő nullával, vagy nem létezik. Ezután, ha f „(x) <0 при х <х0 и f"(х)> 0 X> x0 vagy f „(x)> 0 X <х0 и f"(х) <0 при х> x0. majd M0 (x0. (f (x0)) egy inflexiós pont y = f (x).
Minták kutatási feladatokat
Folytonosság. Aszimptota. Mivel a függvény
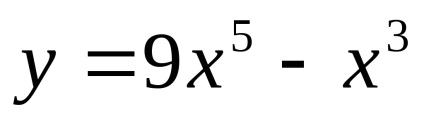

Paritás. Mivel a domain a funkció szimmetrikus nulla, azt találjuk, hogy a következő egyenletek:
. Következésképpen a funkció páratlan. A grafikon szimmetrikus a származás.
A funkció nem periodikus.
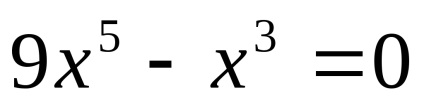
(0; 0);
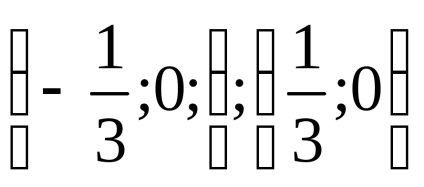
Monoton függvény. Szélsőértékében funkciókat.
2) a folytonosság. Aszimptota. Ez a funkció az összes érték
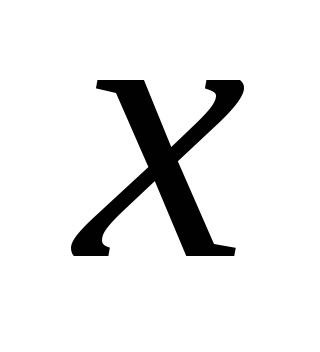
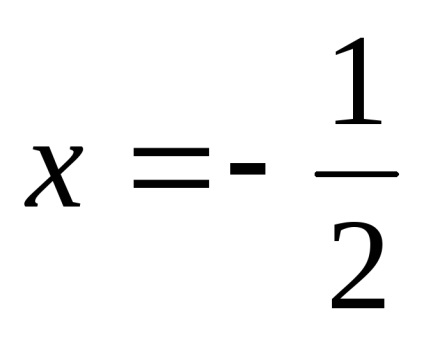
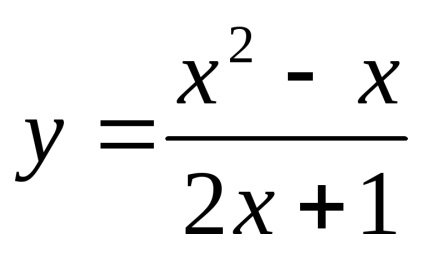
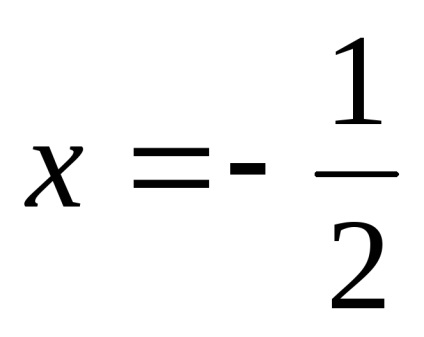
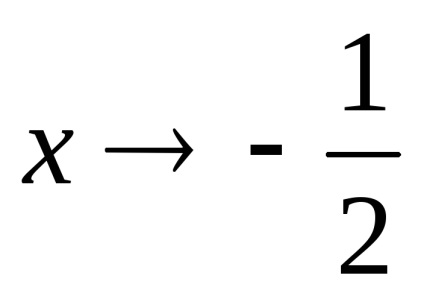
.
.
Következésképpen, a funkció
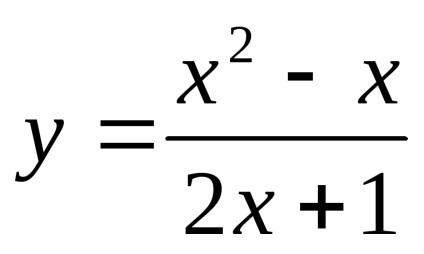
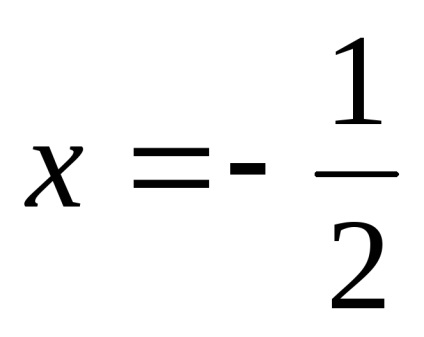
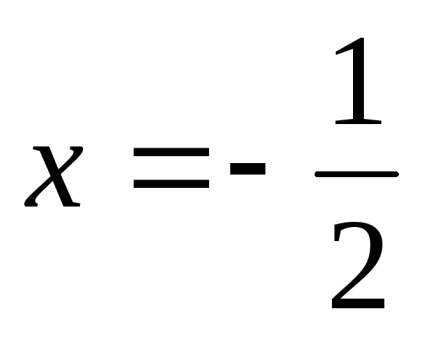
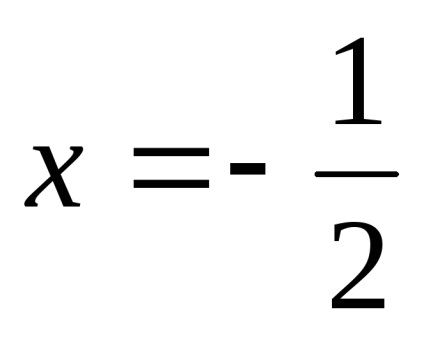
Találunk a lejtőn a asymptote.
Így
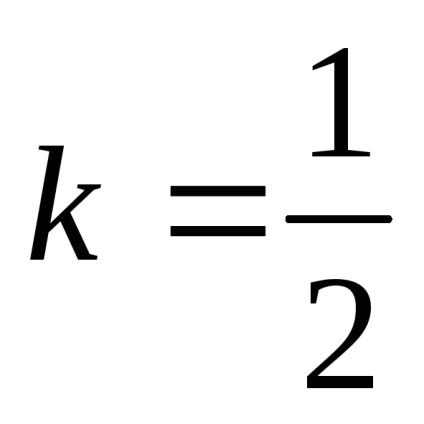
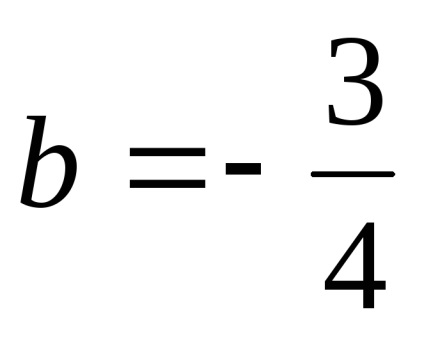
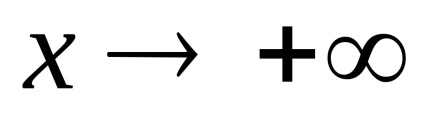
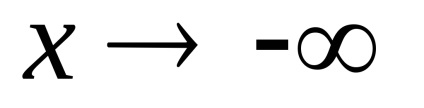
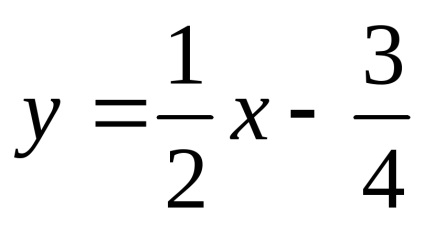
3) paritás. A tartomány definíció nem szimmetrikus nulla, így a funkció sem egyenletes, sem furcsa. az általános formája a funkciót.
4) A funkció nem periodikus.
5) a nullák. y = 0. ha x 2 -x = 0; X (X-1) = 0; x1 = x2 = 0 vagy 1
(0, 0), (1, 0) - grafikon a metszéspontjai a koordinátatengelyek.
6) A monoton. Szélsőérték pont.