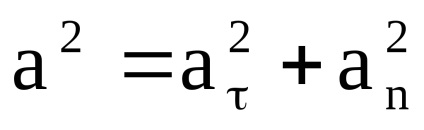Előadás 2 № forgómozgást kinematikája forgómozgást

A legegyszerűbb formája a mozgás mechanikai mozgás. Ez jelenti a változás a testhelyzet vagy annak egyes részei a térben, azaz a egymáshoz képest. A fő feladat a mechanika a válasz arra a kérdésre: hol lesz található a szervezetben mi érdekli az időben.

Bármilyen mozgás a mechanika is képviselteti magát kombinációja két alaptípusát mozgás: fordítás és a forgatást.

Vegyük a legegyszerűbb esetben forgómozgást: a forgatás egy merev test körül egy rögzített tengely körül.

A test azt mondják, hogy teljesen szilárd, ha a távolság a két pont a következetesen. Egyértelmű, hogy ez a fogalom a fizikai absztrakció. Tényleg megfelel ennek a feltételnek, a test, a deformáció lehet hanyagolni az oldatban bizonyos problémákat.

Forgatásával különböző pontjain a szilárd testek mozognak körök, amelyek középpontjai alkotnak egy sort. Ezt a vonalat nevezzük a forgástengely. Ez könnyű észrevenni, hogy a szögelfordulás minden pontján azonos ideig t tehát ugyanaz. Emiatt a forgó helyzetben a test célszerű meghatározni a szöget, amelynél ez képest elfordul a kiinduló helyzetbe. Egyenletben forgómozgást ebben az esetben fog működni  = f (t), amely ugyanolyan alakú minden pontokat a test. Kapunk egy kifejezése ez a funkció általános formában. Erre a célra elegendő, hogy fontolja meg a mozgás az egyik pontot a test tengelye körül.

Legyen egy merev test egy tengely körül forog . A pályája mozgás egy M pont lesz egy kör, amelynek sík merőleges a, 0, és a középpontja ezen a vonalon. A helyzete tetszőleges M pont pályájának-RII uglom fogja meghatározni, hogy mely képez rádiuszvektorhoz , levonni a közepén a kör egy M pont, 0x gerenda. síkjában fekvő kiválasztott röppálya és a viszonyítási pont.

Az SI szögmérés  termelt radiánban. A szöget radiánban 1 - a központi szöge, amely nyugszik az ív hossza egyenlő az R sugár a kör. Ie hogy meghatározza a szöget radiánban szükséges ív hossza osztva görbületi sugara:

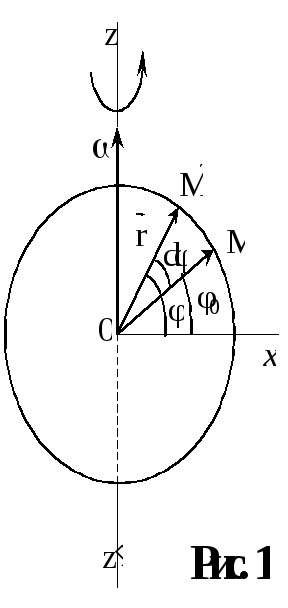
Tekintsük az alapvető kinematikai paramétereit forgó mozgás. Hagyja egy végtelenül kis dt időintervallum anyagi pont a helyről M mozgatjuk

, tompított putds. A sugár vektor Ez kapcsolja be a végtelenül ugold.

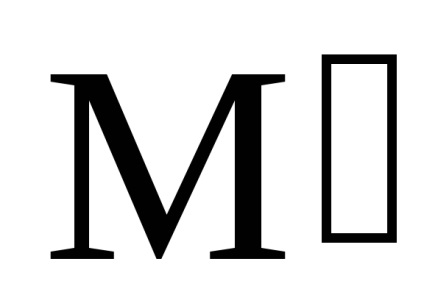
Corner skorost- Ezt a vektort számszerűen egyenlő a elfordulási szög a sugár vektor

egységnyi idő és irány úgy, hogy a hegye mozgását a pont történik az óramutató járásával ellentétes. kezdet Ez azon a ponton O.

Az idő, amely a test teszi egy teljes fordulatot az úgynevezett időszak forgatás (T). mert forgási szög megfelel egy teljes fordulata  = 2 rad, majd egyenletes mozgás

Értéke egyenlő a számát test fordulat per egységnyi idő az úgynevezett forgási frekvenciája n:

Egyenletben egyenletes forgómozgást (ω = const) megoldásával nyerhető a differenciálegyenlet (2):

Ha egyenetlen forgási sebessége változik a szögsebesség jellemzi szöggyorsulással :

a vektor található a forgástengely és úgy irányítjuk, , ha a sebesség növekszik, és az ellenkező irányba, ha a sebesség csökken.

Az általános esetben az egyenlet a egyenletesen gyorsuló forgómozgás (β = const) nyerhető megoldása az differenciálegyenlet

nenie (6) relatív :

használhatja a megszokott lineáris kinematikai paraméterek leírására mozgás körpályán. Például a mozgási sebessége egy pontot a pálya:

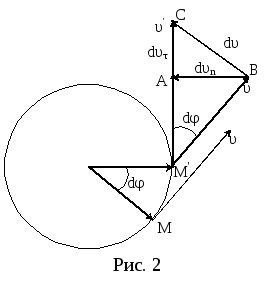
Ez sebessége az átmenet az egyik pont pályája (M) másik (

) Általában változhat mind nagyságát és irányát (2. ábra):

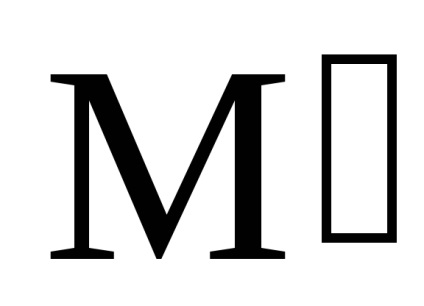
bontsa ki a vektor

két részből áll:- irányított menténés- elvégzése érdekében, hogy. Az ábra azt mutatja, chtodτ -ravna megnöveli eggyel sebességű modul, éshatározza meg a változás az irányt a sebességvektoraz átmeneti ponton a test az M helyzetben, hogy.

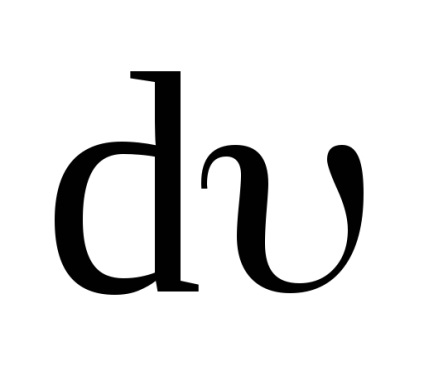
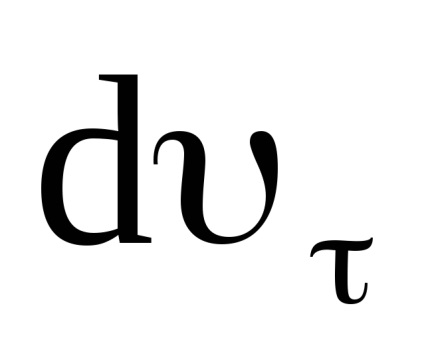
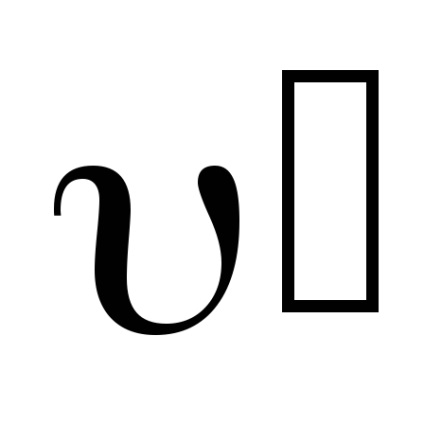
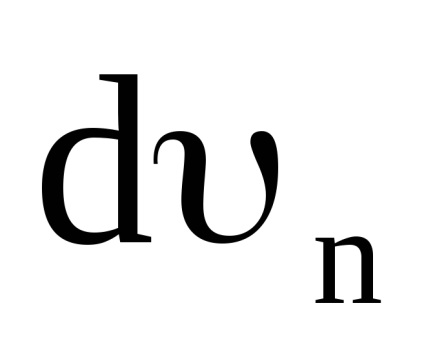
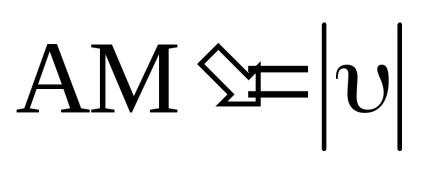
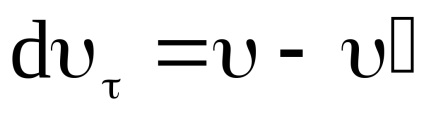
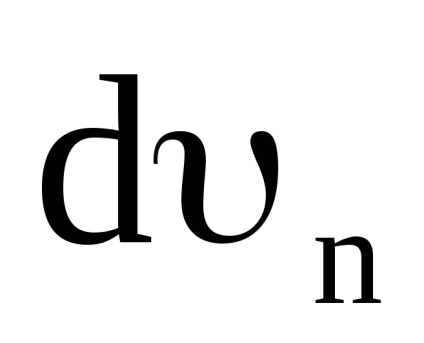
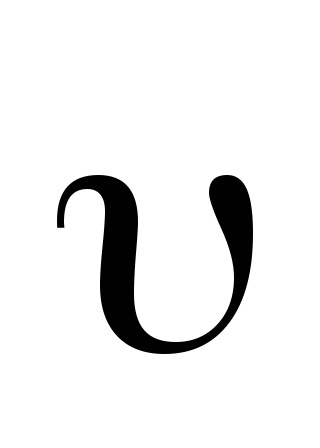
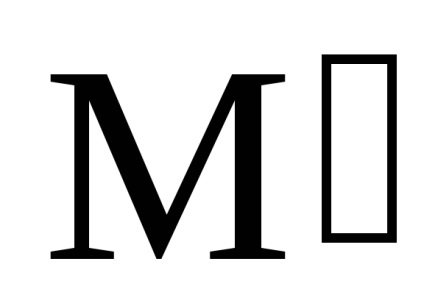
Osztódó (11) dt, megkapjuk:

mert

- egy teljes lineáris gyorsulás, majd (12) átírható

, (13), ahol a- egy tangenciális gyorsulás, amely jellemzi a sebesség a változás mértéke nagyságrendű (abszolút érték); dn / dt = egy - normál gyorsulás, amely meghatározza a „gyors” változási sebessége irányba.

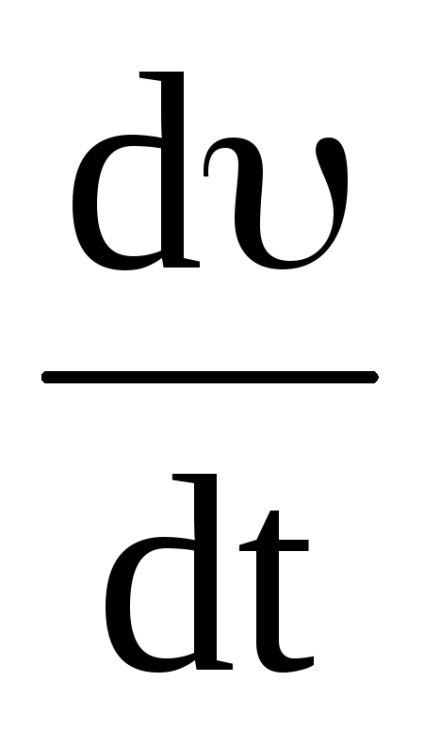
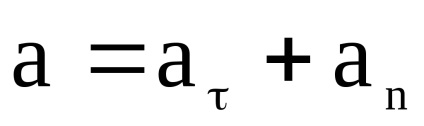
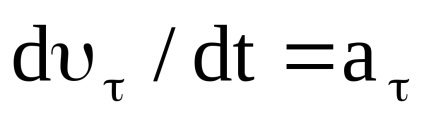
Viszony megalapozására a lineáris és szögmozgás paraméterek kerületileg. A (1) összefüggés

Differenciálás a jobb és bal oldali részén t, van:

Ez a képlet határozza meg a kapcsolatot modul a lineáris sebesség i modul skorosti sarokban. Differenciálás (15) ismét ra, t, megkapjuk a tangenciális gyorsulás:

a háromszög

amikor a radiánban kis szögek:

dn =  · sind =  · d. de

, majd.

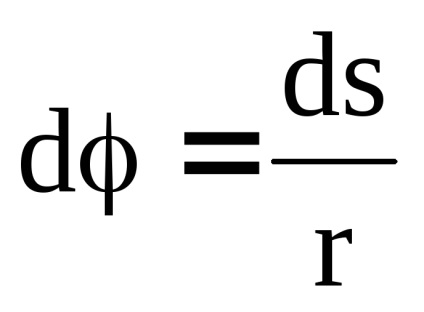
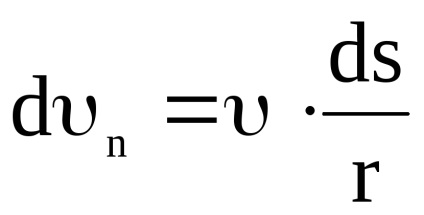
Differenciálás tpravuyu és a bal oldalon az egyenlet, megkapjuk:

Mivel (15) (17) kapjuk:

Tól AVS (dυ) 2 = (dυτ) 2 + (dυn) 2 vagy után osztás (dt) 2 -

. Használata (16) és (18)

Kapcsolódó cikkek

• A forgó mozgás és paramétereit - studopediya

• Hogyan kell kezelni az illegális lerakóhelyek, szakértői hangszóró, a zöld mozgalom az EKA Magyarország

• Azimuths és a mozgás azimut