A nagy számok törvénye
A beállító árnyalattal: BOLSHI`H CHI`SEL ZAKO`N
A nagy számok törvénye - általános alapelv, hatályos to- együttes hatása véletlenszerű tényezők vezet bizonyos nagyon általános feltételek, az eredmény szinte nem függ esélyt. Gyakoriságának hozzávetőleges előfordulása véletlen esemény annak a valószínűsége egyre vizsgálatok száma (Megjegyzendő, hogy először jelenik meg a szerencsejáték) szolgálhat az első példa ennek az elvnek.
A fordulat a 17. és 18. században. Bernoulli [1] bizonyult tétel, amely megállapítja, hogy egy szekvencia független vizsgálatok, amelyek mindegyike a valószínűségét egy bizonyos esemény-cerned A ugyanaz az érték p, 0 <р <1, верно соотношение:
bármikor # 949;> 0, és n → ∞; itt # 956; n - az előfordulások számát az első n kísérletek, # 956; n / n - gyakorisága események. Ezt a Bernoulli-tétel kiterjesztették Poisson C [2] esetében független vizsgálatok, ahol a valószínűsége az esemény A függhet a vizsgálatok számát. Legyen ez a valószínűség a k-adik teszt PK. k = 1, 2, 3, és hagyja, hogy
Ezután Poisson-tétel kimondja, hogy
bármikor # 949;> 0 és n → ∞. Az első szigorú bizonyítás ennek a tételnek kapott P. L. Chebyshevym (1846), az eljárás to- teljesen eltér a Poisson módszer és alapul extrém bizonyos megfontolások; S. Poisson terminál (2) a közelítő képlet mondta valószínűség alapján a használata a Gauss törvény és abban az időben nem feltétlenül érvényes. A C. Poisson először találkozott a „nagy számok törvénye”, hogy szem, hívta általánosítása Bernoulli-tétel.
Természetes további általánosítása Bernoulli tétel és Poisson merül fel, ha tudomásul vesszük, hogy a valószínűségi változók # 956; n leírható összegeként
független véletlen változók, ahol Xk = 1, ha a jelenik meg a k-adik tárgyalás, és Xk = 0 - egyébként. Ebben az esetben a matematikai. elvárás E (# 956; n / n) (. egybeesik a számtani középértéket matematikai elvárások EXk) tömegarány esetén Bernoulli p és p # 175; abban az esetben, Poisson. Más szóval, mindkét esetben kezelt eltérés számtani középértéke számtani átlaga a matematikai. várakozásokat.
A munka P. L. Chebysheva „On középérték” (1867) azt találták, hogy a független valószínűségi változók X1. Xn. arány
(Minden olyan # 949;> 0, és n → ∞) igaz alatt nagyon általános feltételezéseket. P. L. Chebyshev feltételezett matematikai. elvárások EX 2 k összes határolt ugyanaz a konstans, bár egyértelmű bizonyítéka annak, hogy a megfelelőséget követelmény korlátozásokat Xk diszperziók. DXk = EX 2 k - (EXk) 2. vagy követelmények
Így, P. L. Csebisev mutatta a lehetőségét, hogy egy széles általánosítása a Bernoulli tétel. A. A. Markov jegyezni a lehetőséget a további általánosítás, és azt javasolta, hogy használja a nevét B. h. H. általánosítás az összességére Bernoulli-törvény, [és különösen a (3)]. Chebyshev módszer alapja a pontos beállítás általános matematikai tulajdonságait. elvárások és a használata az ún. Csebisev-egyenlőtlenség [valószínűsége (3) ad becslést a forma
ez a határ lehet helyettesíteni pontosabb, persze egy jelentős korlátai cm. Bernstein egyenlőtlenség]. Későbbi bizonyítékok különböző formái B. h. H. eltérő mértékben, amelyek kiterjesztése a Csebisev módszer. . Alkalmazása megfelelő "cut" a véletlen változók Xk (csere kiegészítő mennyiségek X'n, k: H'n, k = Xk ha | Xk - EXk | ≤ Ln és X'n, k = 0, ha | Xk .. - EXk |> Ln, ahol Ln - nek- állandó), A. A. Markov kiterjesztette a órányi B .... az esetekre, amikor a feltételek a diszperziós nem létezik. Pl. azt mutatták, hogy (3) akkor bizonyos állandó # 948;> 0, és L> 0, és valamennyi n
Hasonlóképpen tudjuk bizonyítani a tétel a Khinchin (1929): ha Xn azonos forgalmazási törvények és Exn fenn, a B h s .. (3) teljesül.
Az összegek független véletlen változók lehet formázni egy többé-kevésbé végleges változat B. h. S. Ehhez célszerű menni egy sokkal általánosabb szempontból fogalmához kapcsolódó limit állandóságának szekvenciák valószínűségi változók. Véletlen sorrend értéket Y1. Yn. hívott. nagyon tartós, ha létezik olyan sorozata állandók C1. Cn. hogy bármelyik # 949;> 0 és n → ∞
(.. Ie Yn - Cn nullához "valószínűség", ha (4) van elégedett vele SUCCESSION Cn végezzük, és ahol a CN = mYn MY - a medián a valószínűségi változó Y ..). Továbbá, ahelyett, az X1-szekvencia. Xn. független valószínűségi változók vehet az úgynevezett. Soros áramkör (lásd sorozat áramkör.):
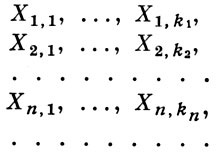
valószínűségi változók (az első index - a gyártási tétel száma, a második - a szám értékét a sorozatban). Véletlen változók minden sorozat feltételezzük, hogy egymástól függetlenek. Reakcióvázlat szekvencia könnyen csökkenthető egy sor rendszer, beállítás k1 = 1, k2 = 2. Xn, k = Xk / n.
Ezután, az általános formája az alkalmazhatóságát B. h. H. összegekre vonatkozó független valószínűségi változók jelentése a következő: a feltételeket, amelyek mellett a maximális összeg Yn állandó?
A válasz erre a kérdésre adtak A. N. Kolmogorov (1928). Tegyük fel, hogy az általánosság elvesztése nélkül, hogy a medián Xn, k egyenlő nullával. Legyen X # 771; n, k = Xn, K | Xn, k | ≤ 1 és X # 771; n, k = 0 | Xn, k |> 1 - Ezután egyidejűleg teljesülnek két feltétel:
Szükséges és elégséges a korlátozó állandó mennyiségű Yn. Ahogy Cn vehet elégségességével ezeket a feltételeket könnyen bizonyítható Csebisov. Ha matematikai. Exn elvárások, k léteznek, akkor könnyen további feltételeket, amelyek mellett lehet választani Cn = EYn. ami a szükséges és elégséges feltételek B. h. s. a klasszikus. készítményben (3). Egy szekvencia független azonos eloszlású véletlen változók n> ezek a feltételek összhangban csökkentett említett Khinchine tétel, egy matematikai létezését. várakozásokat. Ugyanakkor, hogy korlátozza a állandóságát számtani Yn ebben az esetben a szükséges és elégséges feltétele
Ez könnyű példákat adni, ha a feltétel (5) nem teljesül. Tehát ez nem sikerül, ha az összes Xn Cauchy eloszlás sűrűsége 1 / π (1 + x 2) (a raj megfelel a karakterisztikus függvény e - |. T |). Itt a számtani átlag - a jellemző. Funkció E - N [t / n] = e - | t |. és ezért minden n ugyanolyan eloszlású, mint az egyes kifejezések.
A legfontosabb példák, ahol B. h. H. nem kerül sor, meg kell jegyezni, példák kapcsolódó vissza időről időre bolyongás. Pl. egy szimmetrikus Bernoulli véletlen séta idő Tn, hogy az n-edik visszatérés a kiindulási pont az összege n független véletlen változók X1. Xn. ahol X1 - amíg 1. visszatérés, X2 - .. az idő az 1. és 2. megtérülés stb nagyságának eloszlását 2Tn / π n 2 konvergál, ha n → ∞, hogy egy nem degenerált limit törvény sűrűségű
és nullával egyenlő az x ≤ 0. Tehát, ebben az esetben, a megoszlása a számtani középértékeket Xi. t. e. Tn / n, található nagyjából a szegmens hossza nagyságrendileg n (mivel ha alkalmazható B. h. h. koncentrálódik, hosszúságú szegmenst (1)).
ahol az itt következik, hogy amint n → ∞
Egy általánosabb esetben fedezi a kifejezések S. N. Bernshteyna ha dxJ
Korábbi eredmények általánosíthatók különböző irányokban. Először is, a konvergencia látni mindenhol fent „valószínűség”. Tekintsük más típusú konvergencia: .. A készülék négyzetes átlagos valószínűsége, stb (sőt, sok a fenti feltételek biztosítása a konvergencia a négyzetes középértéke egy raj feltételezi konvergenciája valószínűségek). Az ügy a konvergencia egy valószın˝uséggel, fontossága miatt, kiosztott egy speciális úgynevezett „erős a nagy számok törvénye” (lásd. Nagy számban erős törvény).
Továbbá számos tétel tolerálható megfelelő változtatásokat a véletlen vektorok értékeket euklideszi térben bármilyen háromdimenziós szerkezetet, a Hilbert tér bizonyos Banach terek. Így például. ha n> - sorozata független azonos eloszlású véletlen vektorok értékekkel elkülöníthető Banach tér és ha Xn || E || (|| x || - norma x) létezik,
bármikor # 949;> 0 és n → ∞.
Megtekintve a legáltalánosabb formája B. h. S. Ez szorosan kapcsolódik az ergodikus tétel. Természetesen, sok tétel terjeszteni az esetben középen, ahol X (t) - véletlenszerű folyamat attól függően, hogy egy folytonos paraméter (lásd például [10].).
Végül helyett összegek véletlen változók tekinthető más szimmetrikus függvények őket. Ez azért történt, AJ. Hinchinym (1951-1955) kapcsolatban az indokolás egyes statisztikai következtetéseket. Mechanics [9]. Eredmény A. Ya. Hinchina lehet magyarázni a következő konkrét példát. Legyen Xn, Xn 1, n - a koordinátáit vékony, egyenletesen elosztva a felszínen a gömb
Ezután, széles osztálya szimmetrikus függvények f (Xn, Xn 1, n) tartja B. h. S. abban az értelemben, hogy az értékük amint n → ∞ rendkívül konstans [közel van a megjegyzéssel Levy (P. Levy, 1925), hogy kellően rendszeres funkciók egy nagyon nagy számú változó szinte állandó a legtöbb domain].
A legtöbb régi kézi kiterjedt statisztikai. adatok illusztráló B. h. s. (Lásd. Pl. [4], [11]).
Irod [1] Bernoulli J. Ars conjectandi, opus posthumum, Basileae, 1713 (. Az orosz fordítás - Negyedik rész készítmények Bernoulli SPB 1913 ..); [2] Poisson S.-D. Recherches sur la probabilit # 233; des jugements en mati # 232; újra criminelle et en mati # 232; újra civile, PR # 233; CED # 233; ES des r # 232; GLES g # 233; n # 233; hörgést du calcul des probabilit # 233; s, P. 1837; [3] Teljes Csebisov PL. cit. Op. t 2, M. - L. 1947 .; [4] Markov A. A. fogkő a valószínűség, 4th ed. M. 1924 [5] Bernshteyn S. N. Valószínűségelméleti, 4th ed. M. - L. 1946 [6] Gnedenko BV Kolmogorov A. N. határeloszlását összegekre független véletlen változók, M. - L. 1949. [7], J. Oak. Sztochasztikus folyamatok, Amer. az angol. M. 1956; [8] W. Grenander valószínűségek algebrai struktúrák sávban. az angol. M. 1965 [9] J. A. Szimmetrikus Xinchin funkciót többdimenziós felületeken, a könyvben. Memória A. A. Andronova, M. 1955 o. 541-74; [10] M. Loeve, valószínűségszámítás, transz. az angol. M. 1962 [11] Uspensky J. V. Bevezetés a matematikai valószínűsége, N. Y. - L. 1937.
- Matematikai Lexikon. T. 1 (A - D). Ed. Board: I. M. Vinogradov (fejezetek szerk) [et al.] - M. "szovjet Encyclopedia" 1977, 1152 col. illusztrációkkal.